
T&C LAB-AI
Robotics
Probabilistic Robotics
Map Building
양정연
2020/12/10
1
T&C LAB-AI
Robotics
What is a Map or Mapping
2

T&C LAB-AI
Robotics
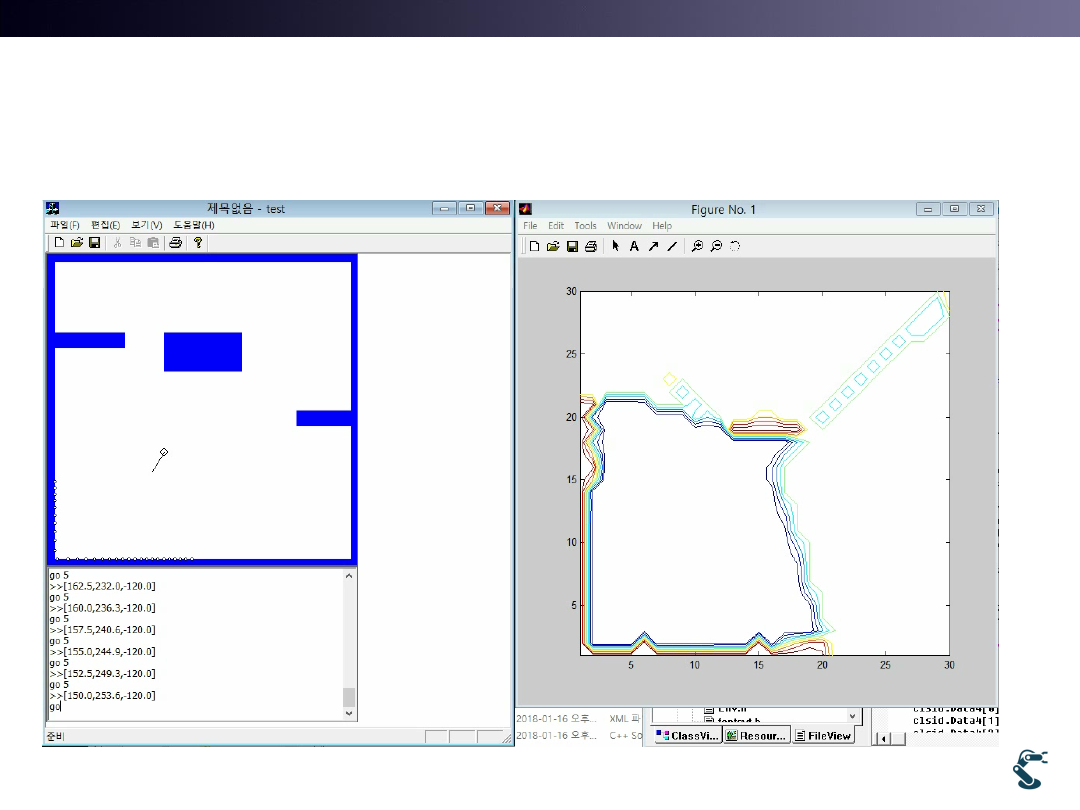
Introduction: Manual Mapping
3

T&C LAB-AI
Robotics
Map Drawings with Pen and Eraser
4
Wrong
Fix it

T&C LAB-AI
Robotics
Problems of Map Drawing
• 1. Distance is NOT Clear with a Video.
• 2. Wrong Position should be Fixed later
• 3. “Stair” is unclear
• 4. Missing Area
• 5. Noisy Area
5

T&C LAB-AI
Robotics
Problems of Map Drawing
• 1. Distance is NOT Clear with a Video.
• 2. Wrong Position should be Fixed later
• 3. “Stair” is unclear
• 4. Missing Area
• 5. Noisy Area
6

T&C LAB-AI
Robotics
Problems of Map Drawing
• 1. Distance is NOT Clear with a Video.
• 2. Wrong Position should be Fixed later
• 3. “Stair” is unclear
• 4. Missing Area
• 5. Noisy Area
7

T&C LAB-AI
Robotics
Engineering Ways:
Map has these Problems
• 1. Distance Problem
– Distance measurement ( or Distance metric ) is possible with a
laser scanner or Kinect-like point cloud devices
• 2. Update Map (Unclear, Missing and Noisy area)
– With a Single video, we missed most of map information
– Thus, map update is very essential (like pencil with eraser)
• 3. Where am I?
– In spite of all, The current position information is missing.
8

T&C LAB-AI
Robotics
Goal of SLAM is,
• SLAM: Simultaneous Localization and Mapping
– It is NOT Easy doing localization and mapping at the same
time
– Localization requires Map
– Mapping requires Localization
– It is an egg-and-hen problem
9
0:
1:
1:
(
,
|
,
)
t
t
t
p x
m z u
Observation
Control input
Map
position
T&C LAB-AI
Robotics
Rao-Blackwellization
• Doing Factorization
10
0:
1:
1:
(
,
|
,
)
t
t
t
p x
m z u
1:
1:
0:
1:
1:
( |
,
) (
|
,
)
t
t
t
t
t
p m x
z
p x
z u
By Murphy in 1999
Mapping
Localization
SLAM
Rao-Blackwell-
Kolmogorov
Theorem

T&C LAB-AI
Robotics
Mapping from Rao-Blackwellization
• Mapping
– Assumption
– If we know X, then observation Z with X can generate a
Map
• Then, How to generate a map?
– The Easiest one is using a GRID map
Occupancy Grid Mapping
11
1:
1
0:
1:
1:
:
(
,
( |
)
|
)
,
t
t
t
t
t
p x
z u
p m x
z
T&C LAB-AI
Robotics
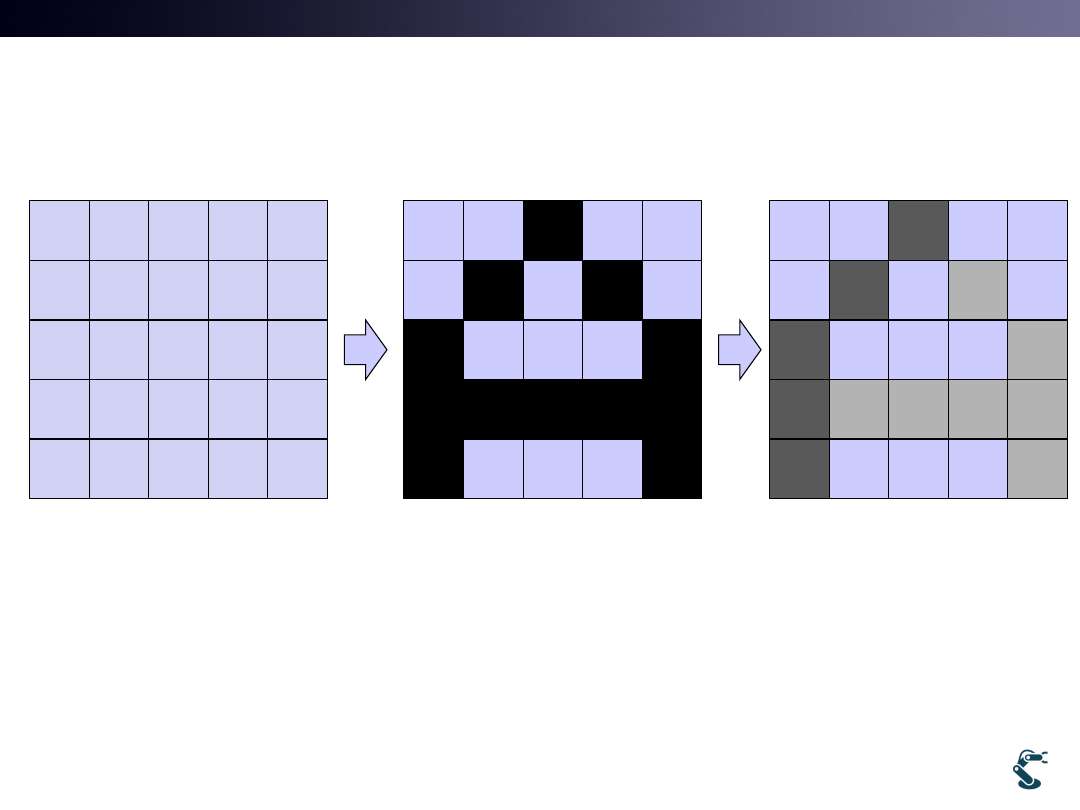
Occupancy Grid Mapping
• Prob. Of occupancy :
12
Empty space
0 for empty
1 for occupancy
Probabilistic way
0< Prob. of occupancy<1
0 : empty
(
)
1:
,
i
p m
occupied
otherwise

T&C LAB-AI
Robotics
Each Grid is Independent
13
m1
m2
m3
m4
m6
m5
m25
1
2
25
( )
(
)
... (
)
p m
p m p m
p m
25
1
( )
(
)
i
i
p m
p m
Probability is always not greater than 1.
Thus, multiplication becomes very smaller.
Logarithmic operation must be used.
25
1
log ( )
log
(
)
log( (
))
i
i
i
i
m
p
p m
p m
1:
1:
0:
1:
1:
:
(
|
,
)
( |
,
)
t
t
t
t
t
RB
p x
z u
p m x
z
1:
1:
1:
1:
( |
,
)
from (
|
,
)
i
t
t
t
t
p
x
z
p
x
m
z
m
Calculate P(m) from p(mi)

T&C LAB-AI
Robotics
Probability of a Cell Occupancy
14
1:
1:
1:
1:
(
|
,
)
( |
,
)
i
t
t
t
t
p m x
z
p m x
z
( , , )
( , , ) ( , )
( , | )
( | , ) ( | )
( )
( , )
( )
p A B C
p A B C p B C
p A B C
p A B C P B C
p C
p B C
p C
• Remind Bayesian Rule
1:
1:
1:
1: 1
(
|
,
)
(
|
,
, z )
i
t
t
i
t
t
t
p m x
z
p m x
z
( ,
| )
( | , )
( | )
p A B C
p A B C
P B C
T&C LAB-AI
Robotics
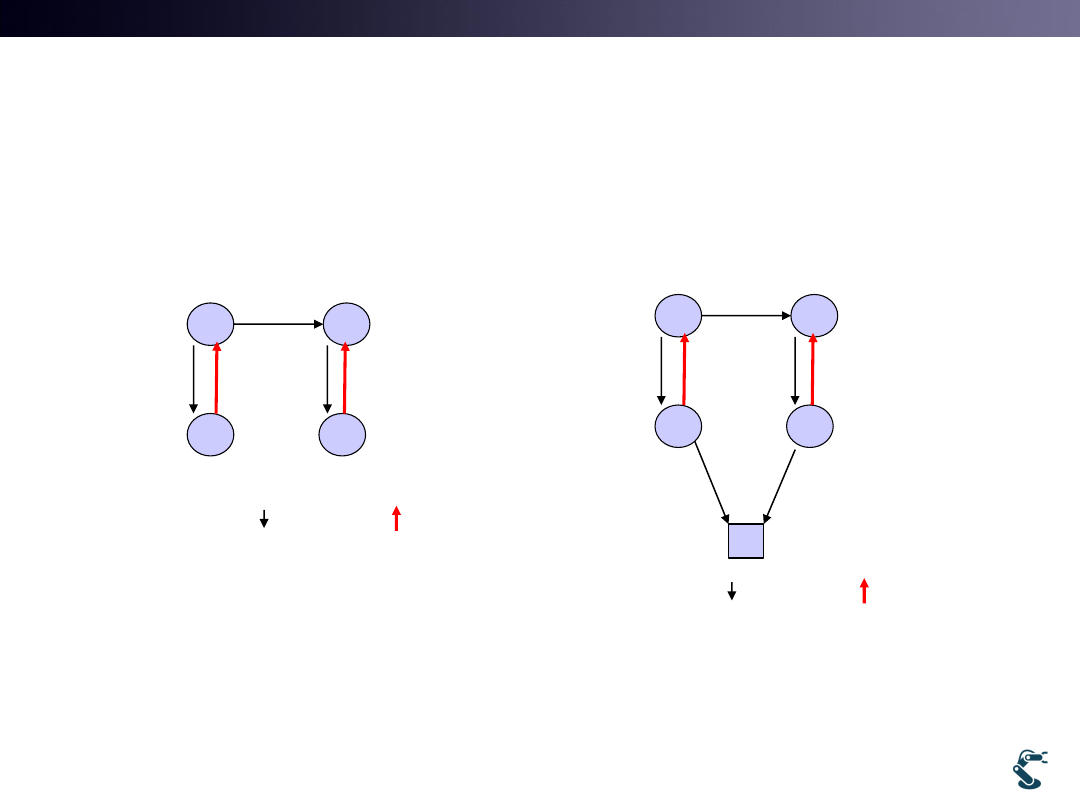
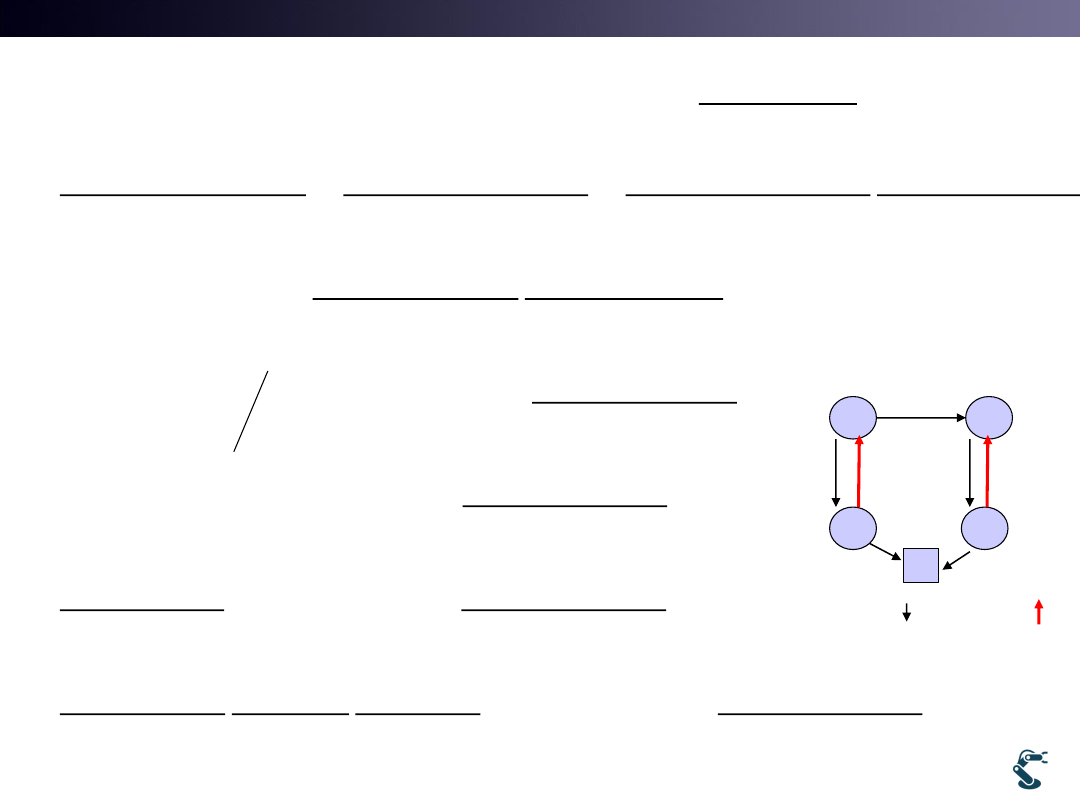
Remind that Map is update through
the kth step
15
Xk-1
Xk
Zk-1
Zk
Causal
Estimation
Xk-1
Xk
Zk-1
Zk
Causal
Estimation
mi
T&C LAB-AI
Robotics
16
1:
1:
1:
1: 1
1:
1: 1
1:
1: 1
1:
1: 1
1:
1: 1
1:
1: 1
1:
1: 1
1:
1: 1
1:
1: 1
1:
1
(
|
,
)
(
|
,
, z )
(
,
,
, z )
(z ,
,
,
)
(z ,
,
,
) (
,
,
)
(
,
, z )
(z ,
,
)
(
,
,
)
(z ,
,
)
(z |
,
,
i
t
t
i
t
t
t
i
t
t
t
t
i
t
t
t
i
t
t
i
t
t
t
t
t
t
t
t
i
t
t
t
t
t
t
i
t
p m x
z
p m x
z
p m x
z
p
m x
z
p
m x
z
p m x
z
p x
z
p
x
z
p m x
z
p
x
z
p
m x
z
1:
1: 1
1:
1: 1
: 1
1:
1: 1
1:
1: 1
1: 1
1: 1
1: 1
1:
1: 1
1: 1
1: 1
1:
1: 1
1:
(
,
,
)
(
,
)
)
(
,
)
(z ,
,
)
1
(z |
, ,
) p(m |
,
)
(z |
,
)
1
(z |
, ) p(m |
,
)
(z |
,
)
(z ,
, )
p(m |
(
, )
i
t
t
t
t
t
t
t
t
t
t
t
i
t
t
i
t
t
t
t
t
t
i
t
i
t
t
t
t
t
t
i
t
i
i
t
p m x
z
p x
z
p x
z
p
x
z
p
m x z
x
z
p
x
z
p
m x
x
z
p
x
z
p
m x
x
p m x
1
1: 1
1:
1: 1
1: 1
1: 1
1:
1: 1
1
,
)
(z |
,
)
(
, z , ) ( , )
( )
1
p(m |
,
)
(z , )
(x )
(
, )
(z |
,
)
t
t
t
t
t
i
t
t
t
t
t
i
t
t
t
t
t
i
t
t
t
t
z
p
x
z
p m
x
p z x
p x
x
z
p
x
p
p m x
p
x
z
( ,
| )
( | , )
( | )
p A B C
p A B C
P B C
Xk-1
Xk
Zk-1
Zk
Causal
Estimation
mi
T&C LAB-AI
Robotics
17
1: 1
1: 1
1:
1: 1
1: 1
1: 1
1:
1: 1
1: 1
1: 1
1:
(
, z , ) ( , )
( )
1
p(m |
,
)
(z , )
(x )
(
, )
(z |
,
)
( |
) p(m |
,
)
(
| z , )
(
|
)
(z |
,
)
( |
) p(m |
,
)
(
| z , )
(
)
(z |
i
t
t
t
t
t
i
t
t
t
t
t
i
t
t
t
t
t
t
i
t
t
i
t
t
i
t
t
t
t
t
t
i
t
t
i
t
t
i
t
t
p m
x
p z x
p x
x
z
p
x
p
p m x
p
x
z
p z x
x
z
p m
x
p m x
p
x
z
p z x
x
z
p m
x
p m
p
x
1: 1
,
)
t
z
Xk-1
Xk
Zk-1
Zk
Causal
Estimation
mi
1:
1
1: 1
1: 1
: 1
1:
1:
( |
)
(
| , )
(
)
( |
,
(
|
,
)
(
)
)
|
,
t
t
i
t
t
i
t
i
t
t
i
t
t
t
t
p z x
p m x z
p m
p
p m x
z
p m x
z
z x
z
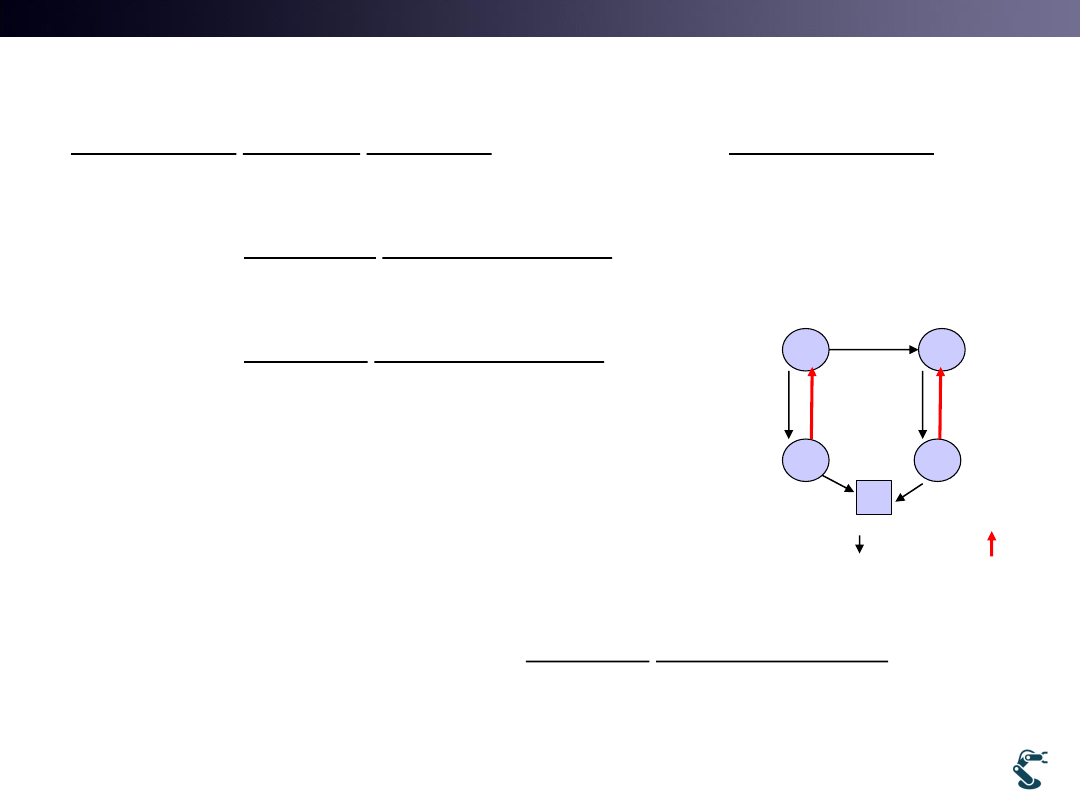
Map mi is associated with the
combination of x and z,
But not with x.
1:
1:
1:
1: 1
(
|
,
)
(
|
,
, z )
i
t
t
i
t
t
t
p m x
z
p m x
z

T&C LAB-AI
Robotics
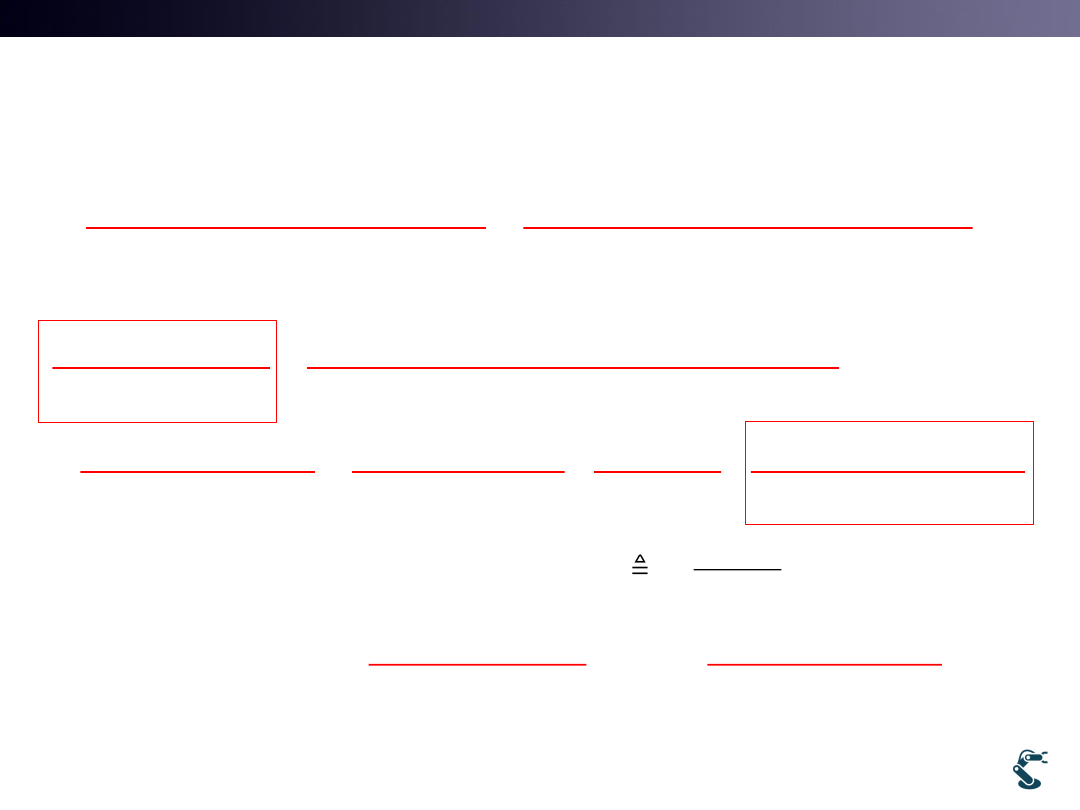
Binary Attribute of “Occupancy or Empty”
Simplify the Equations
• Occupancy
• Empty
• We do NOT calculate “BLUE” probability
18
1: 1
1: 1
1:
1
1
1
1
:
:
:
( |
)
(
(
|
|
(
|
,
)
(
|
,
)
)
,
)
(
)
,
i
t
t
i
i
t
t
i
t
t
t
t
t
t
t
p m x
p z x
p z x
p m x
z
z
p
p
z
m
z
m
x
1: 1
1: 1
1
1
:
:
1:
1:
1
(
(
| , )
( |
)
(
|
,
)
(
|
,
|
,
, "
)
)
)
(
"
i
t
t
t
t
i
t
t
i
t
t
t
t
i
t
p z x
p z
p
m x
z
p
m
p
m x z
x
z
N
z
m
x
t
p
o
1:
1:
1:
1: 1
1: 1
1:
1:
1:
1: 1
1
1: 1
(
|
,
)
(
|
,
)
(
|
( |
)
(
,
)
(
|
,
(
)
(
| , )
(
)
(
|
,
)
, )
|
)
t
t
t
i
t
t
i
t
t
i
t
t
i
i
t
t
i
i
t
t
t
t
t
i
t
p m x
z
p m x
z
p
m x
p z x
p z x
z
p
m
p m
p m x z
p
m
p
m x z
x
z
z
T&C LAB-AI
Robotics
Log Odds Notation
19
1:
1:
1:
1:
1: 1
1: 1
1: 1
1: 1
(
|
,
)
(
(
)
(
)
(
| , )
(
| ,
|
,
)
(
|
,
)
(
|
,
)
)
i
t
t
i
t
t
i
t
t
i
i
i
t
t
t
i
t
i
t
t
p m
p
m
p m x z
p
m x
p m x
z
p
m x
z
p m x
m x
z
z
p
z
1:
1:
1: 1
1: 1
1:
1:
1: 1
1: 1
1:
1:
1: 1
1: 1
1:
1:
(
| , )
(
)
(
(
|
,
)
(
|
,
)
(
|
,
)
(
|
,
)
(
|
,
)
(
|
,
)
1
| , )
(
)
(
| , )
1
(
)
1
(
| , )
(
|
,
)
(
)
(
1
i
t
t
i
t
t
i
t
t
i
t
i
t
t
i
i
t
t
i
i
t
t
i
i
t
t
i
t
i
t
t
i
t
t
i
t
t
p m x z
p
m
p
m x z
p
p m x
z
p m x
z
p
m x
z
p
m
m
p m x z
p m
p m x z
p
x
z
p m x
z
p m x
z
p m x
z
p
m
1: 1
1: 1
|
,
)
i
t
t
m x
z
1:
1:
1:
1:
1:
1:
1:
1:
1:
1:
1:
1: 1
1:
:
1
1
(
|
,
)
(
|
,
)
(
|
,
)
1
(
|
,
log
(
|
,
)
log
log
(
|
,
)
(
| , )
(
)
|
,
)
i
t
t
i
i
t
t
i
t
t
t
i
t
t
i
t
t
i
i
t
t
t
i
t
t
odds representation
l m x
z
l m x
z
l m x z
l m
l m x
p m x
z
p m x
z
p
m x
z
p m x
z
z
( )
log
: ( )
log
1
( )
p a
odds l a
p a

T&C LAB-AI
Robotics
Finally, Grid Map Probability
20
1:
1:
1: 1
1: 1
(
|
,
)
(
| , )
|
,
(
)
i
t
t
i
t
t
i
t
t
i
l m x
z
l m x z
l m x
z
l m
( )
log Odds : ( )
log
1
( )
p a
l a
p a
( )
( )
( )
( )
( )
( )
( )
1
( )
( )(1
)
1
( )
1
1
1
l a
l a
l a
l a
l a
l a
p a
e
p a
p a
e
e
e
p a
e
e
1:
1:
1:
1:
1
(
|
,
) 1
1 exp (
|
,
)
i
t
t
i
t
t
p m x
z
l m x
z

T&C LAB-AI
Robotics
Summary
• Goal of SLAM
• Rao-Blackwellization
• Map building
• Map has binary attribute : occupancy grid map
• Map probability
21
0:
1:
1:
(
,
|
,
)
t
t
t
p x
m z u
1:
1:
0:
1:
1:
( |
,
) (
|
,
)
t
t
t
t
t
p m x
z
p x
z u
1:
1:
( |
,
)
t
t
p m x
z
1:
1:
1:
1:
( |
,
) or (
|
,
)
t
t
t
t
p m x
z
p
m x
z
1:
1:
1:
1:
1
(
|
,
) 1
1 exp (
|
,
)
i
t
t
i
t
t
p m x
z
l m x
z

T&C LAB-AI
Robotics
What is the Physical Meaning of
Occupancy grid map?
• P(m)=0 means, “I am sure that it is an Empty”
• Thus, when we start mapping, the initial prob. = 0.5
22
( )
log Odds : ( )
log
1
( )
p a
l a
p a
m
m
1:
1:
(
|
,
)
0
i
t
t
p m x
z
1:
1:
(
|
,
) 1
i
t
t
p m x
z
1:
1:
(
|
,
)
?
i
t
t
p m x
z
t=0
At
t>0
At
(
)
0
i
p m
(
) 1
i
p m
(
)
?
i
p m
0
(m)
(m)
log
0
( )
0.5
1
(m)
p
l
p m
p

T&C LAB-AI
Robotics
Map Update Strategy
with Inverse measurement(or Sensor) model
• If we calculate , then we update a map
• It is called
– From the current position, x and the current measurement, z,
we estimate prob. Of whether a map mi is empty or occupied.
It is different with a classification probability.
23
1:
1:
1: 1
1: 1
1
0
1
0
(
|
,
)
(
| , )
|
,
(
)
(
| , ) l
(
| , ) l
i
t
t
i
t
t
i
t
t
i
t
i
t
t
t
i
i
t
t
t
l m x
z
l m x z
l m x
z
l m
l
l m x z
l m
l m x z
l
1:
1:
0
0 : (
|
,
)
0 : (
)
i
t
t
t
i
t
p m x
z
l
t
p m
l
(
| , )
i
t
t
l m x z
(
| , )
(
| , )
Inverse measurement model
i
t
t
i
t
t
l m x z
p m x z
1:
1:
( |
,
)
t
t
p m x
z
T&C LAB-AI
Robotics
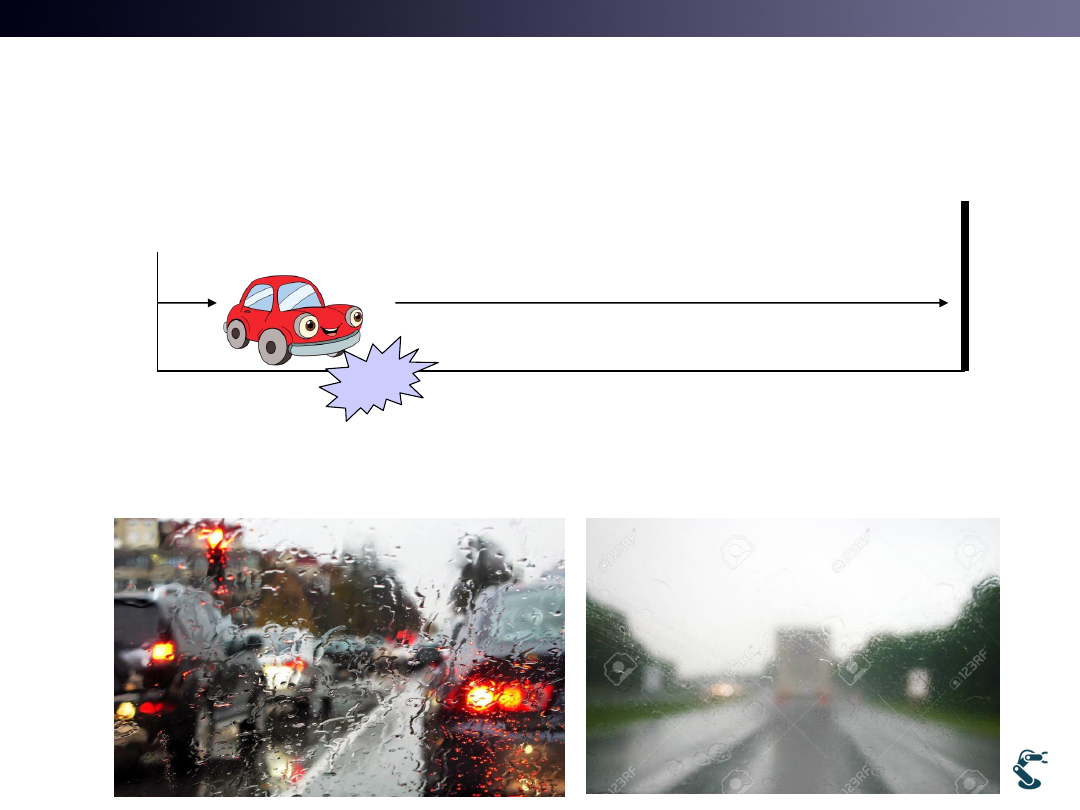
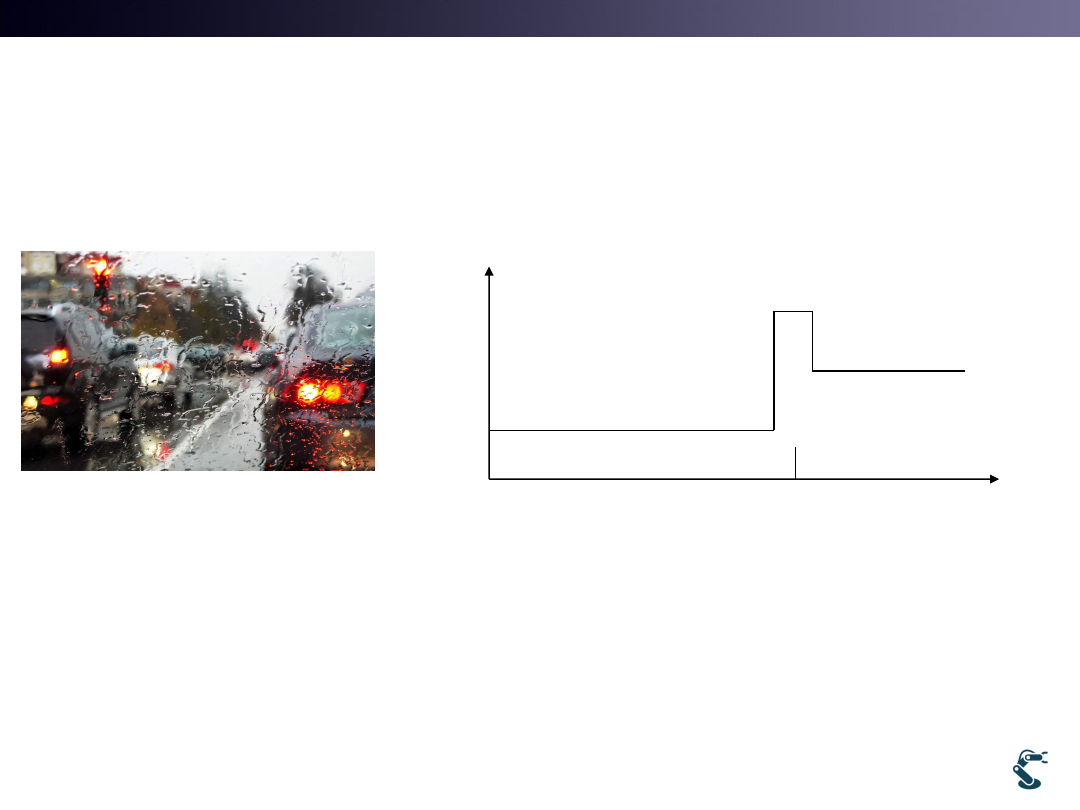
Why Inverse Sensor Model is required?
24
x
z
wall
slip
Our measurement, z has noise
T&C LAB-AI
Robotics
Inverse Sensor Model
• Prob. of occupancy z=10, prob(m|x,z) = 0.8
• Prob. Of occupancy z=5, prob(m|x,z) = 0.2
• Inverse sensor model is dependent of Sensor itself 25
distance
Prob. Of occupancy, p(x)
0.2
Measurement:
Distance is 10m
10m
0.8
T&C LAB-AI
Robotics
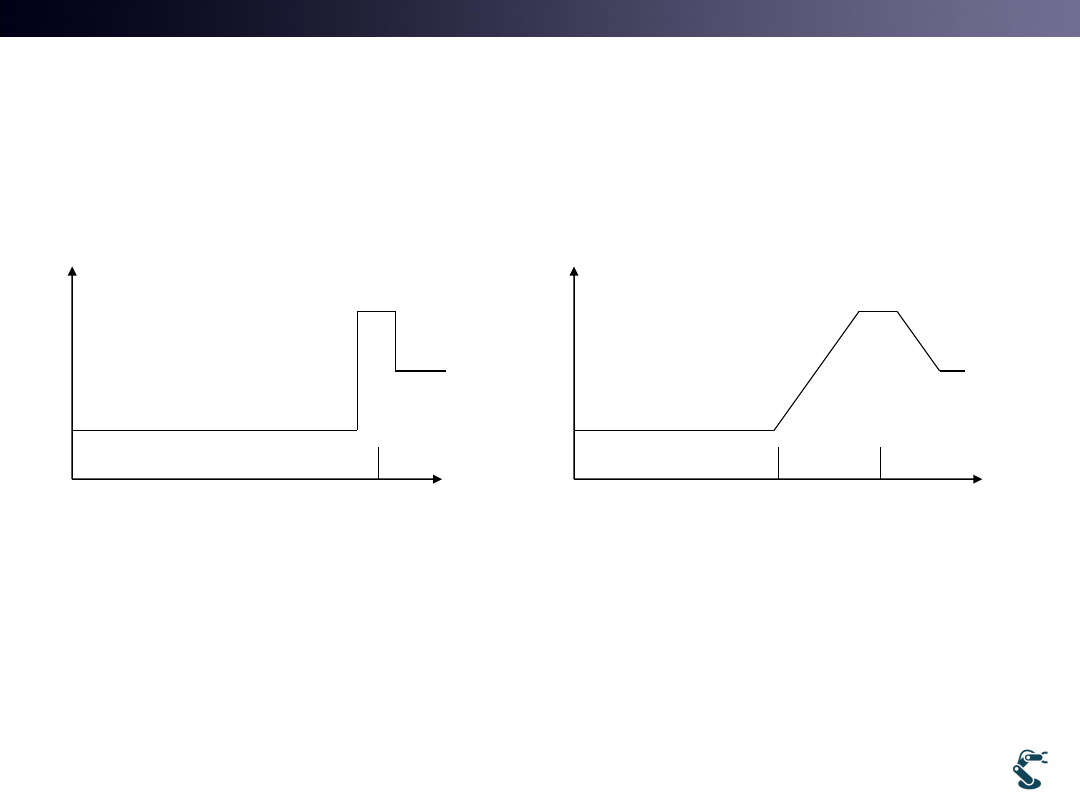
Inverse Sensor Model :
Sensor Performance
26
distance
Prob. Of occupancy
0.2
10m
0.8
distance
0.1
10m
0.9
• Which one is better?
• Case B has poor performance over 7m.
– The sensor does not determined whether it is occupied or
not over 7m
Case A
Case B
7 m
Prob. Of occupancy
T&C LAB-AI
Robotics
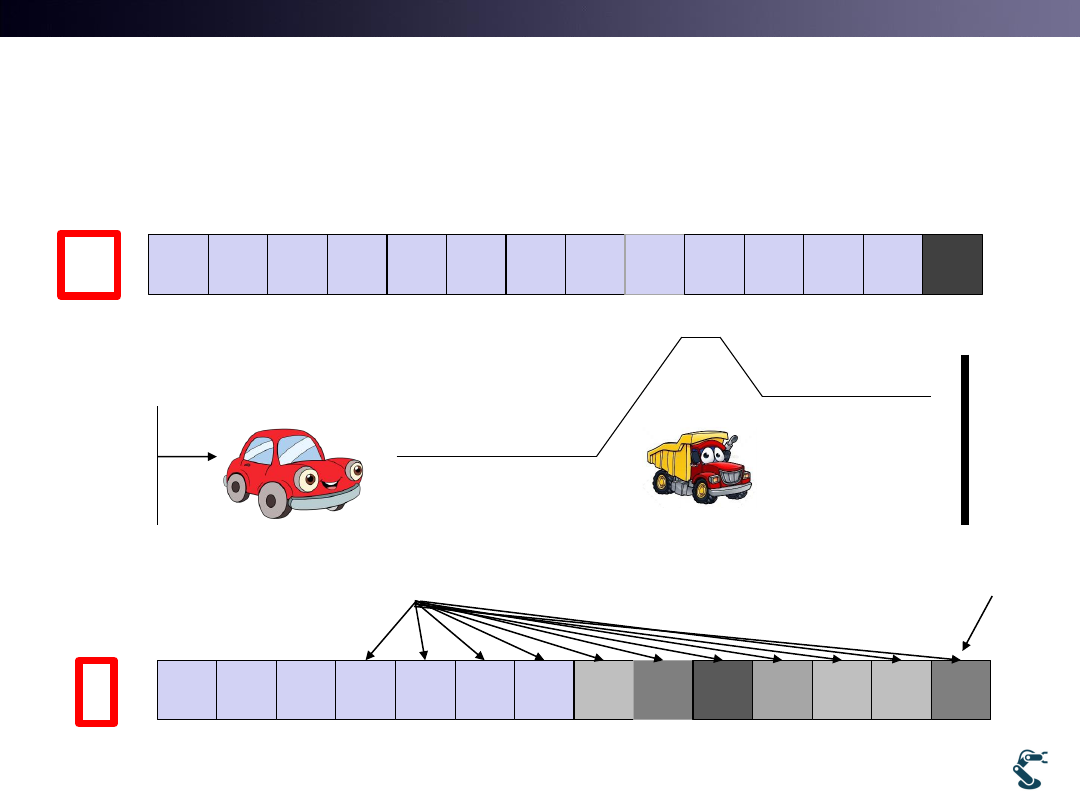
Why Inverse S.M. is so Important?
And is Not a Recognition Rate?
27
x
z
10m
7 m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
1
0
(
|
, ) l
t
i
t
t
t
l
l m x z
l
m
m
m
m
m
m
m
m
m
m
m
m
m
m
1
t
l
t
l
p(
| , )
i
t
t
m x z
Goes
brighter
No
changes
T&C LAB-AI
Robotics
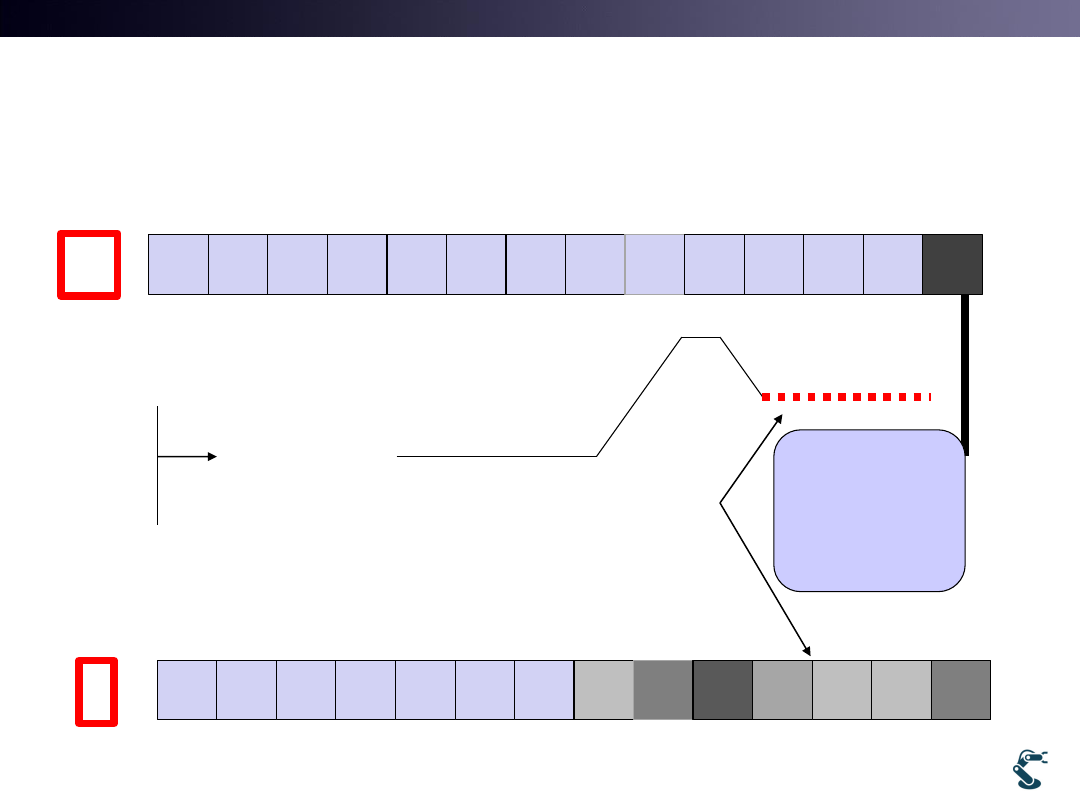
What is the meanings of Inverse S.M.
beyond an obstacle?
28
x
z
m
m
m
m
m
m
m
m
m
m
m
m
m
m
1
0
(
|
, ) l
t
i
t
t
t
l
l m x z
l
m
m
m
m
m
m
m
m
m
m
m
m
m
m
1
t
l
t
l
p(
| , )
i
t
t
m x z
We don’t know
beyond the truck
But,
It might be a wall

T&C LAB-AI
Robotics
Inverse S.M. is different
with Recognition Rate
• Recognition rate tells us,
– It has a probability of whether it is true or not
• Inverse Sensor(or Measurement) model tells us,
– NO interest about whether an obstacle is or not
– I am very interested in WHERE an obstacle is now?
– Probability of distance is the major interest. P = P(x)
29
Distance, x
P(x)
0.1
0.9
Case B
T&C LAB-AI
Robotics
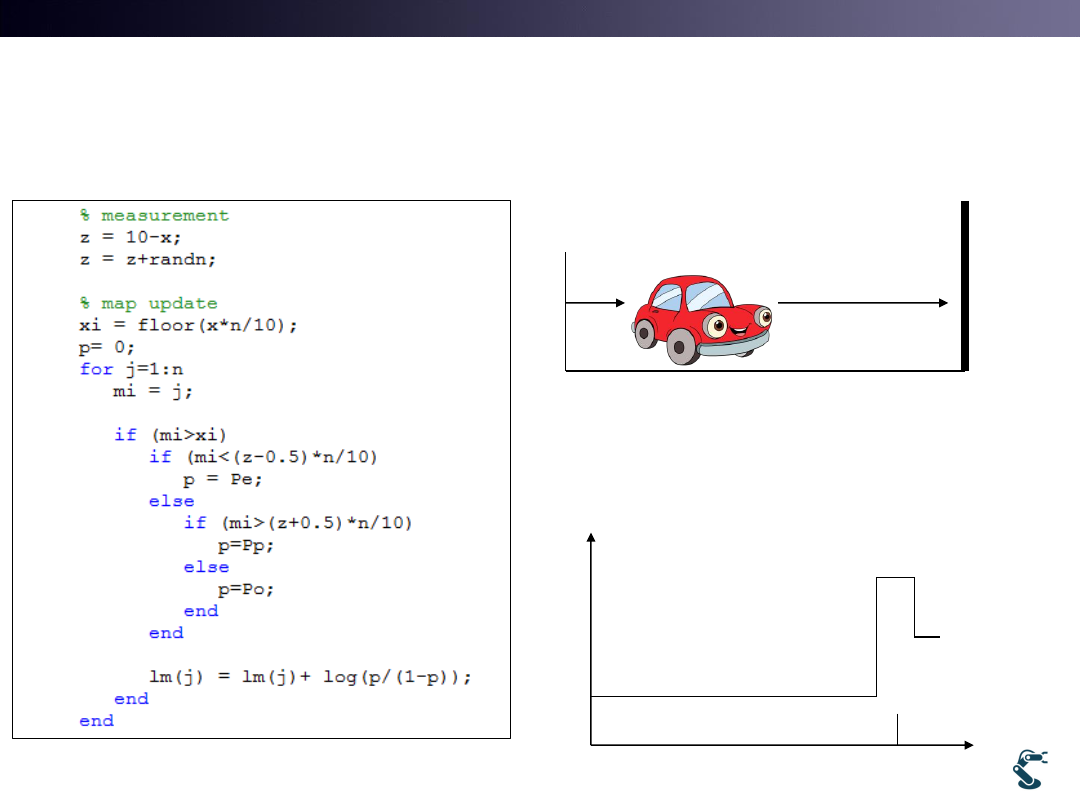
Simulation: Test.m
30
x
z
1
0.5 (0,1)
k
k
x
x
N
10
(0,1)
z
x N
Inverse Sensor Model
0.2
d
0.8
0.5
1
Tough
Noise!
T&C LAB-AI
Robotics
1
2
3
4
5
6
7
8
9
10
0
0.5
1
1.5
Position,X
k
x
0
10
20
30
40
50
60
70
80
90
100
-10
-5
0
5
log odd=l(m)
map,mi
l(
m
)
0
20
40
60
80
100
120
0
0.5
1
Pr(m)
map,mi
P
r(
m
)
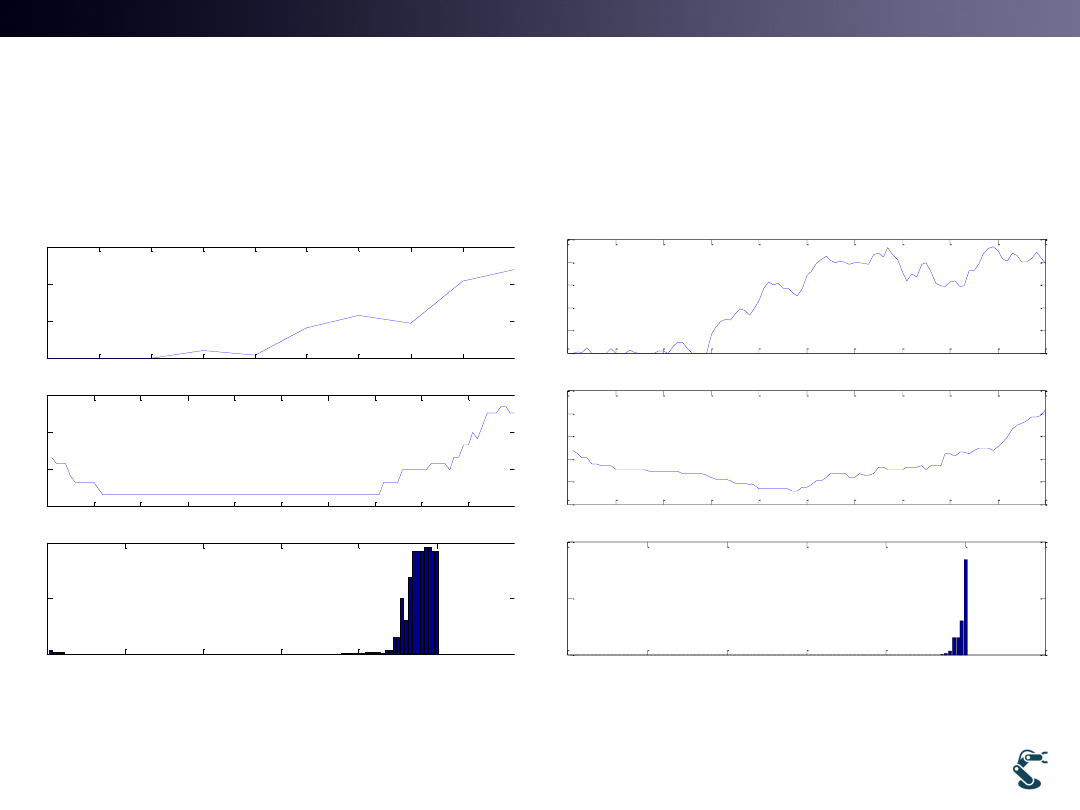
Simulation Result
31
0
10
20
30
40
50
60
70
80
90
100
0
2
4
6
8
10
Position,X
k
x
0
10
20
30
40
50
60
70
80
90
100
-40
-30
-20
-10
0
10
log odd=l(m)
map,mi
l(
m
)
0
20
40
60
80
100
120
0
0.5
1
Pr(m)
map,mi
P
r(
m
)
t=0 to 10
t=0 to 100
Wall
becomes
clearer
T&C LAB-AI
Robotics
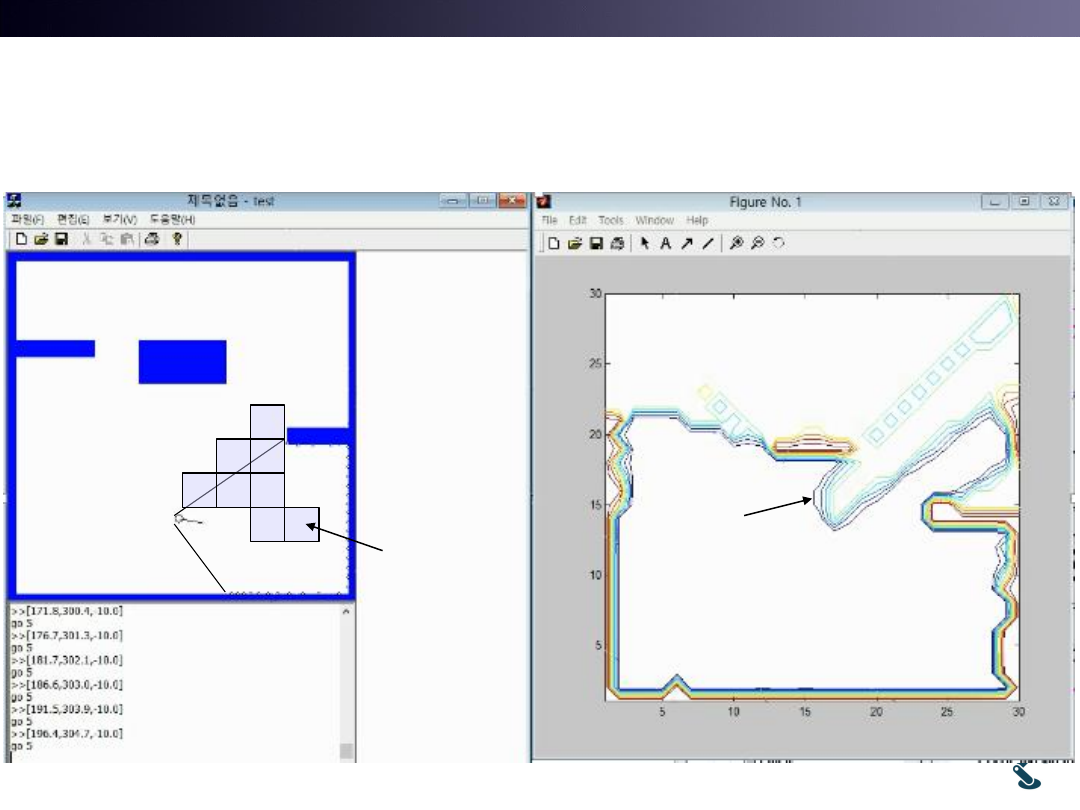
Extends from 1D to 2D
What will be required?
32
P(m)>Pempty
Update map