
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Computer Graphics and Programming
Lecture 3
Perspective Projection Matrix
Jeong-Yean Yang
2020/10/22
1
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
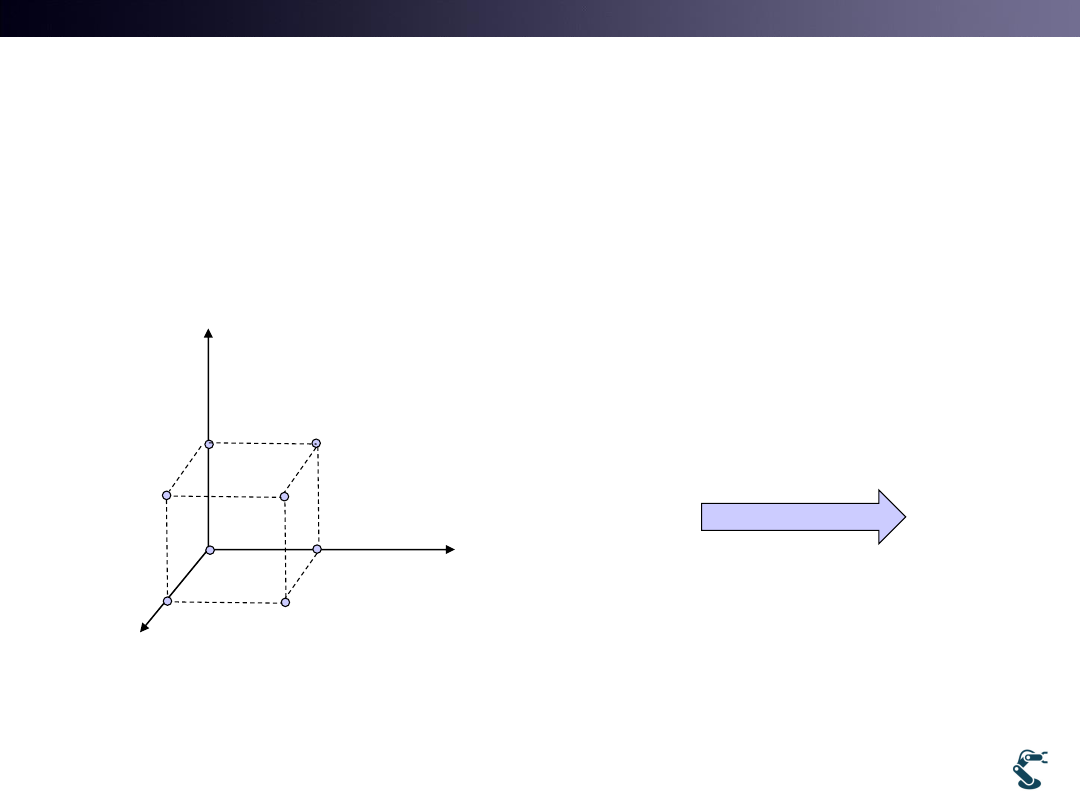
Projection from 3D into 2D
• Think box in 3D
2
z
x
y
0
1
2
3
4
5
6
7
P0= [0,0,0]
P1=[1,0,0]
P2=[1,0,1]
P3=[0,0,1]
P4=[0,1,0]
P5=[1,1,0]
P6=[1,1,1]
P7=[0,1,1]
Homogeneous
Transform, H
P0’
P1’
P2’
P3’
P4’
P5’
P6’
P7’
Question: How we get 2D points for line drawing?
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
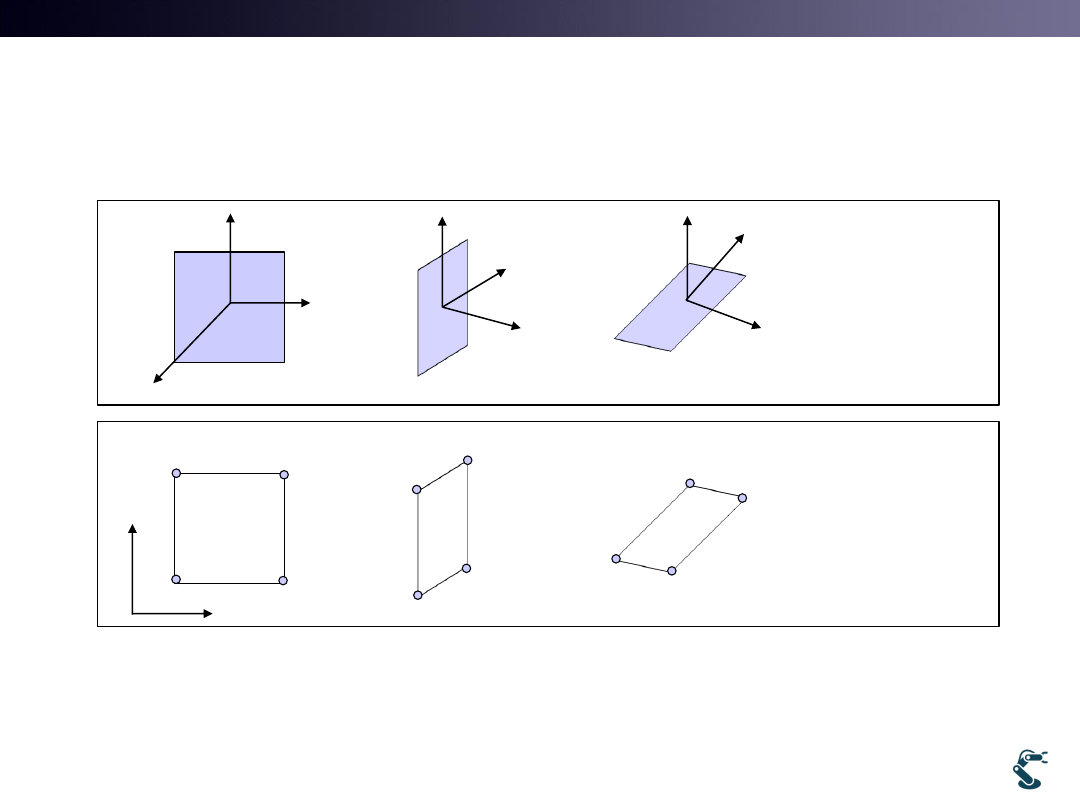
Box Projection onto 2D Space
• Projection: Mapping from N dimensional space
to N-1 dimensional space
3
3D
Transform
2D vertices
are needed!!

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Ref. Projection in Machine Learning
• Information in a High dimensional space is projected
onto a lower dimensional space
– Why? 4 wheels, engine, and so on.
• Starting point for Structuring Hierarchy
4
Car!
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
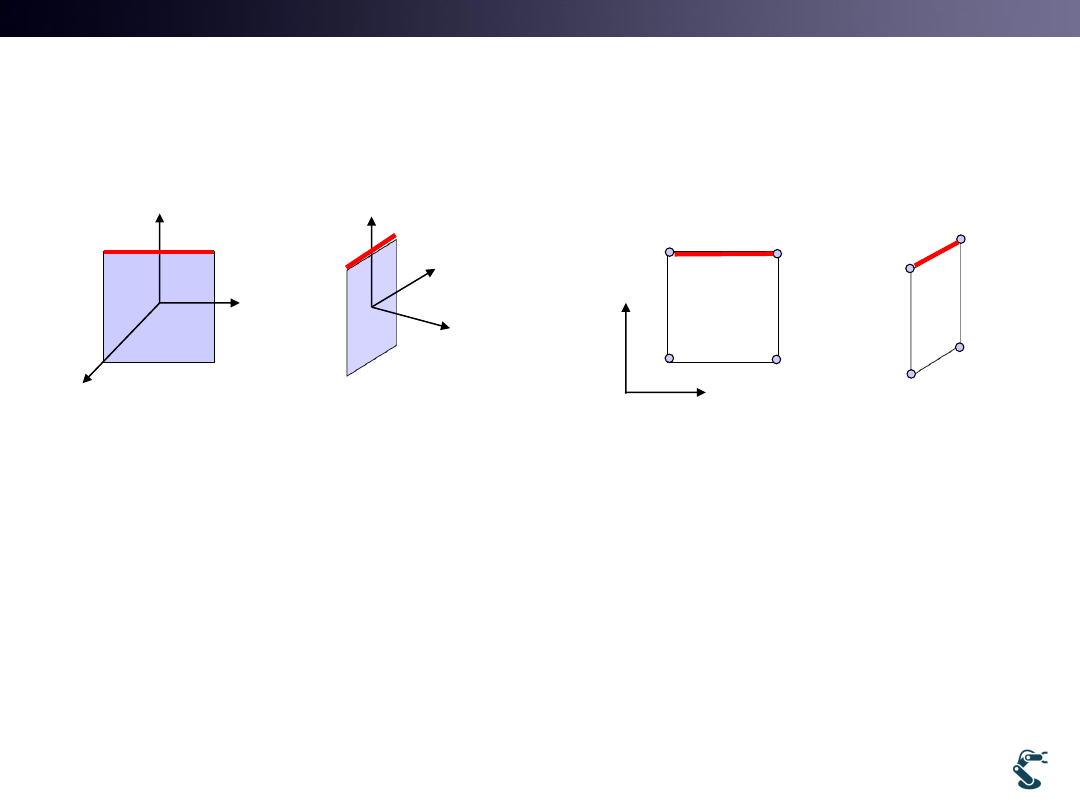
Characteristics of Projection
• 3D Space is a Euclidean Space.
• But, Projected Space is NOT a Euclidean Space.
5
A
B
A
B
A’
B’
A’
B’
||
|| const
A B
||
'
' || const
A
B
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
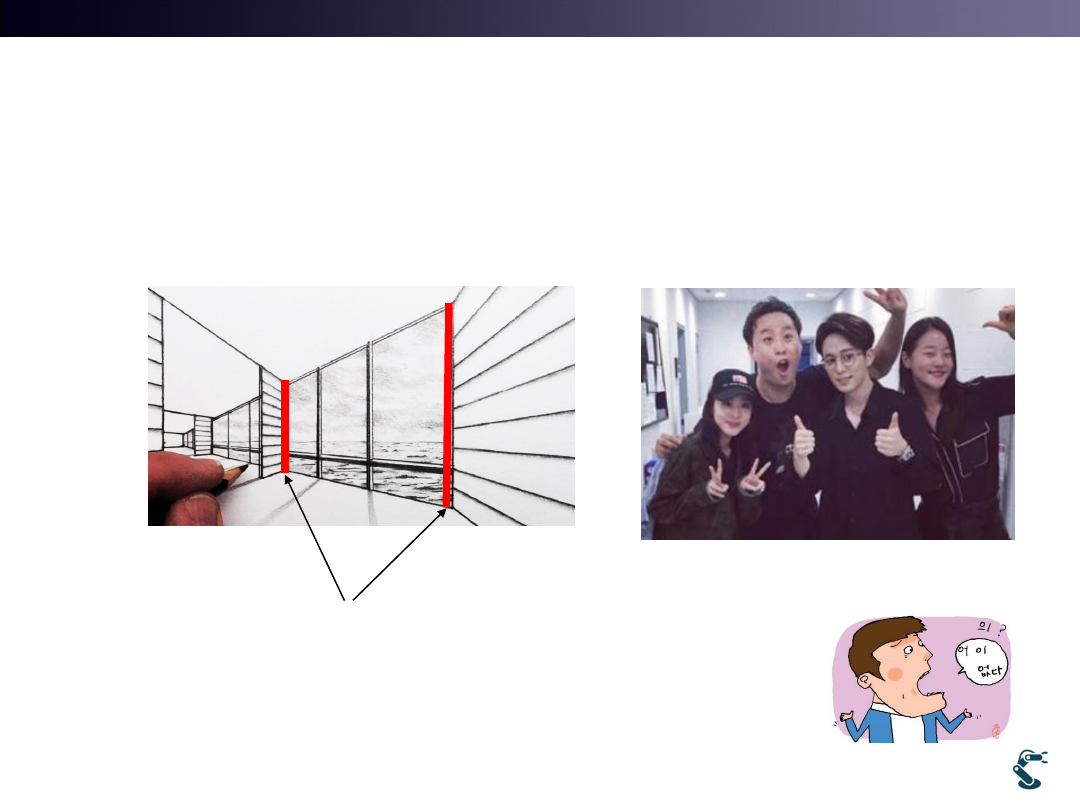
Perspective Projection Matrix
• Perspective View
6
Two lines have Same Distance,
but these look Different in Perspective View
Who is the closest one?
It is not clear….
Big head…

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Back to Homogeneous Transform
Why we call Homogeneity, 1?
• We learn X has 1, which is needed for Homogeneous
transform.
• Why 1 is required?
7
0
1
R
T
H
1
x
X
'
0
1
0
1
1
1
R T
R T
x
Rx T
X
HX
X

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Homogeneity, 1 for Projection
• In a Homogeneous Space,
– It is NOT a general vector space
– It is a Affine Space
8
2
1
2
x
x
hx
X
h
Everything looks same!

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Vector or Point
• Homogeneous Transform requires
9
h=0 or 1
x
X
h
1
2
1
2
1
2
1
2
1
2
,
1
1
1 1
0
x
x
X
X
x
x
x
x
X
X
Point-Point = Vector
1
2
1
2
1
2
1
2
,
0
0
0
x
x
X
X
x
x
X
X
Vector-Vector = Vector

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Definition of Vector and Point
• So, 0 or 1 is the only case?
• It is a Point.
10
,
, Point, P
0
1
x
x
Vector V
P
0.3
x
What is it?
/ 0.3
P
0.3
1
x
x
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
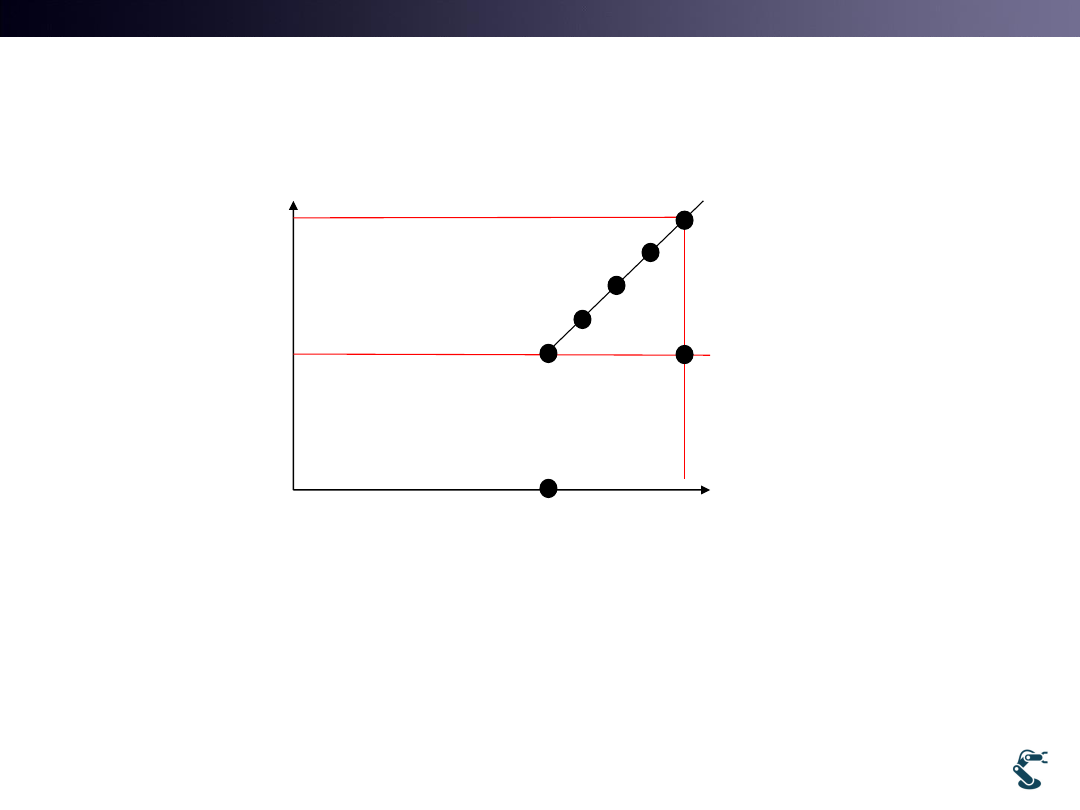
Truth of Homogeneous Transform
• In a Homogeneous Space,
– Design this space as,
– Every Vector is projected on h=0
– Every point is projected on h=1
11
ˆx
0
ˆx
X
h
h=1
h=0
0
ˆx
h=2
0
ˆx
0
ˆ
2x
0
0
0
ˆ
ˆ
ˆ
2
0.1
1
2
0.1
x
x
x
X
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
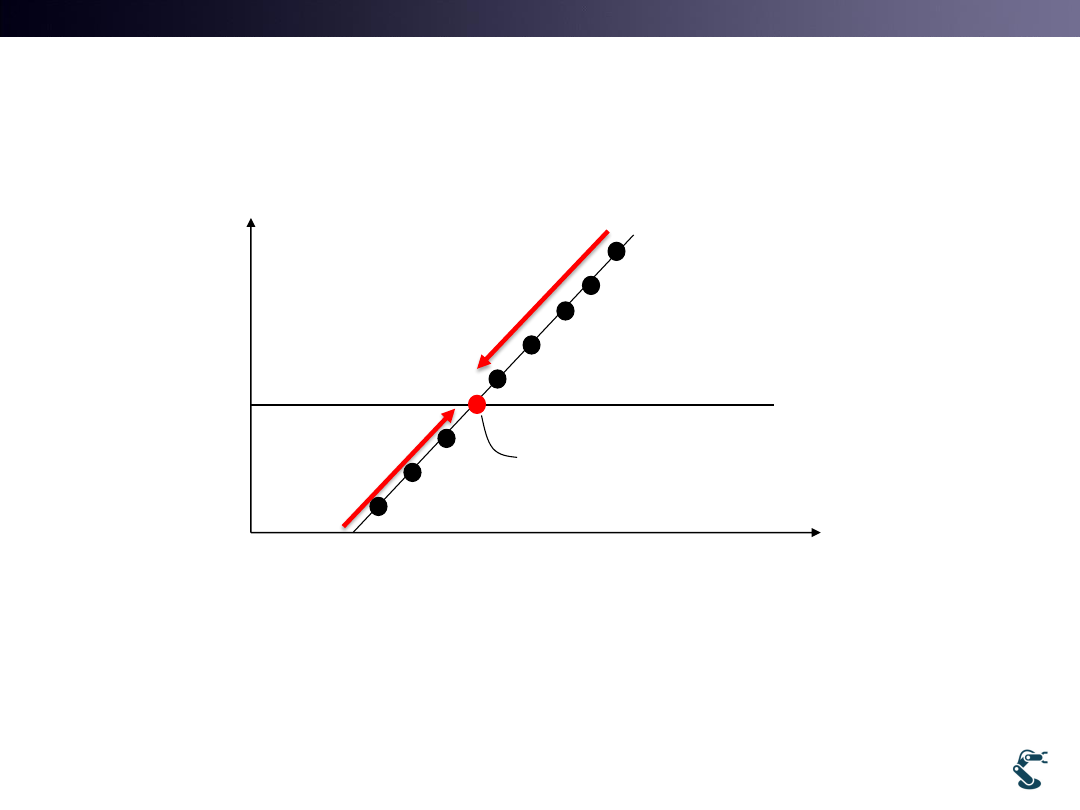
Homogeneous Projection on h=1
• All points passing
are same.
• All points passing
are projected on
12
h=1
ˆx
ˆ
( ,1)
x
ˆ
(
, )
hx h
ˆ
( ,1)
x
ˆ
(
, )
hx h
ˆ
( ,1)
x
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
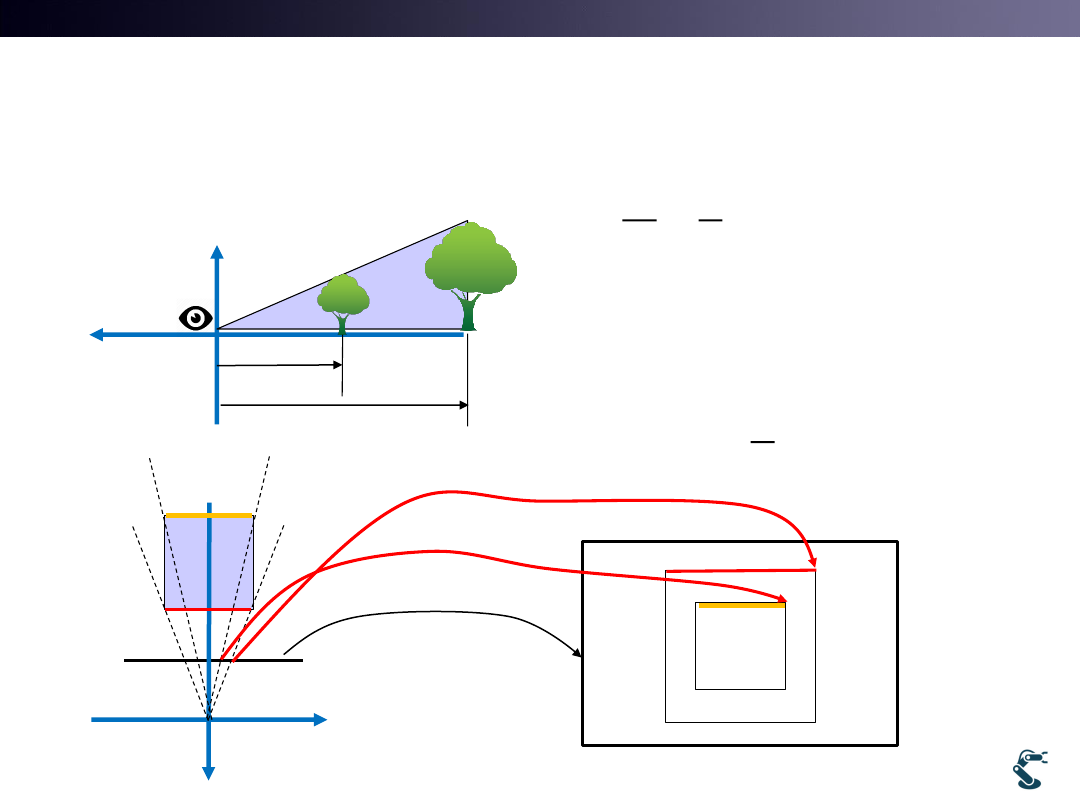
Example) Perspective View
13
Z
X
x
'
x
'
z
z
'
(z', z<0)
'
we define '
-1,
'
(z<0)
x
x
z
z
if
z
x
x
z
Z
X
'
1
z
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
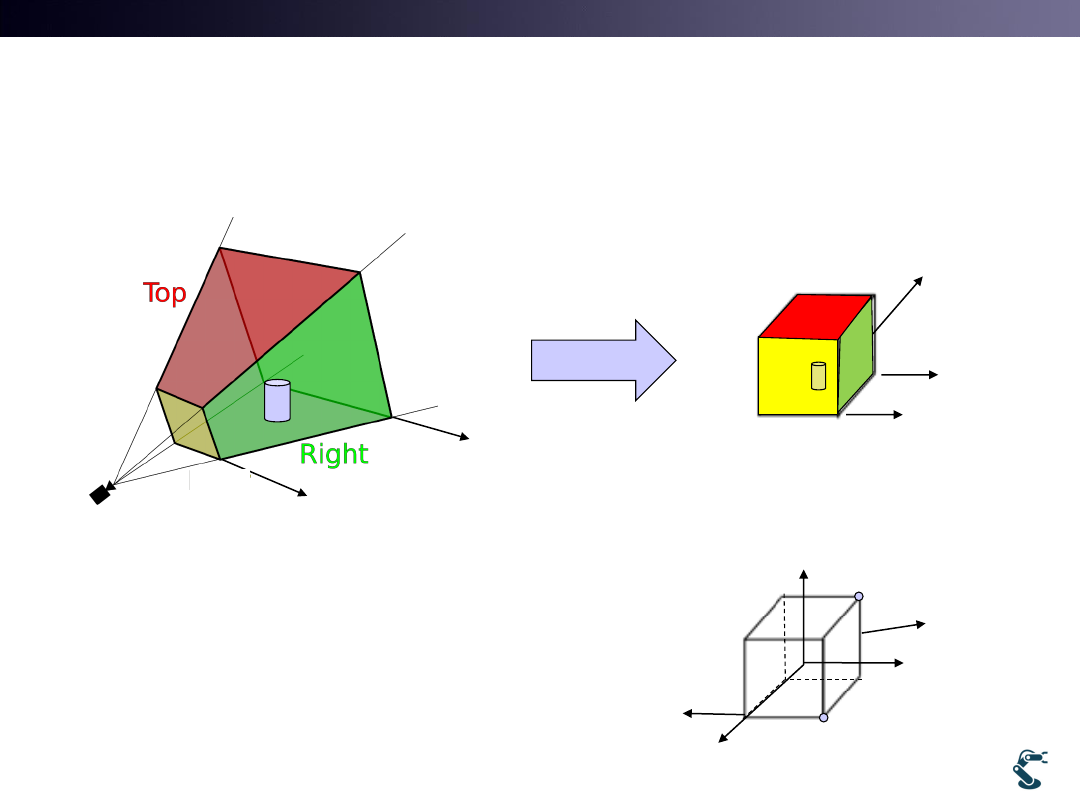
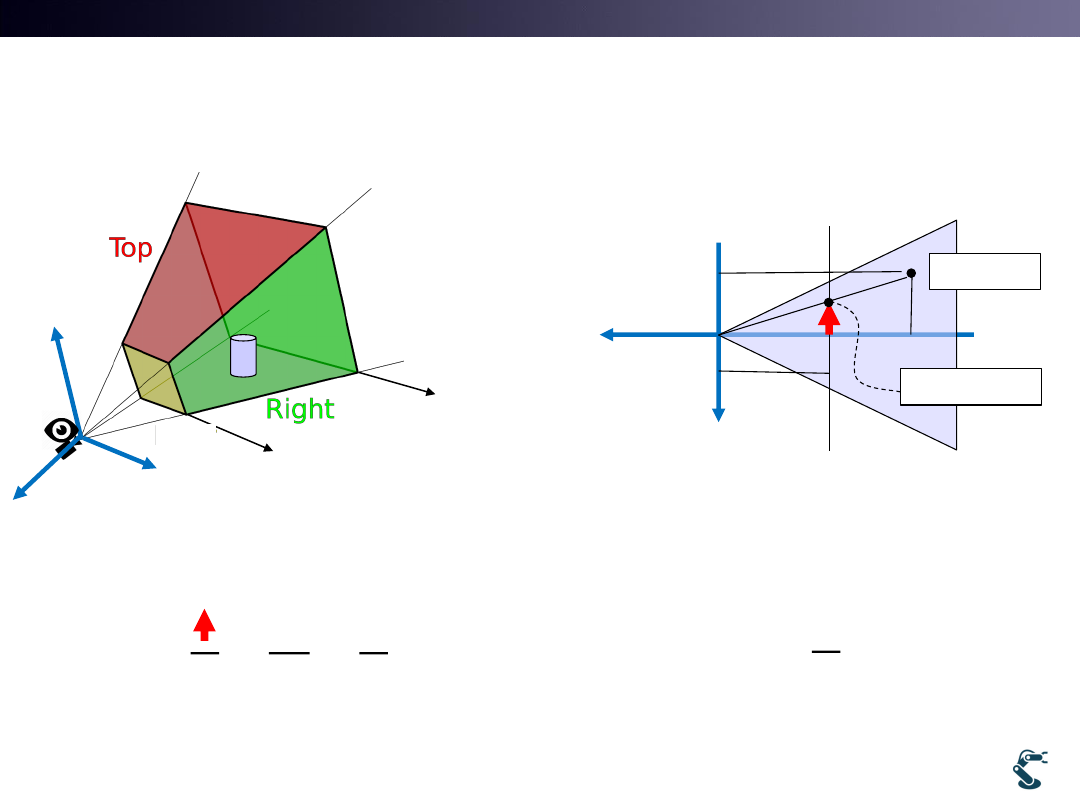
Modeling of Perspective View
uses Viewing Pyramid(Frustum)
14
3D Space
Unit Space
W=H=T=[-1,1]
Near
Far
Near
Far
z
x
y
(1,1,-1)
(1,-1,1)
Near
Far
z
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
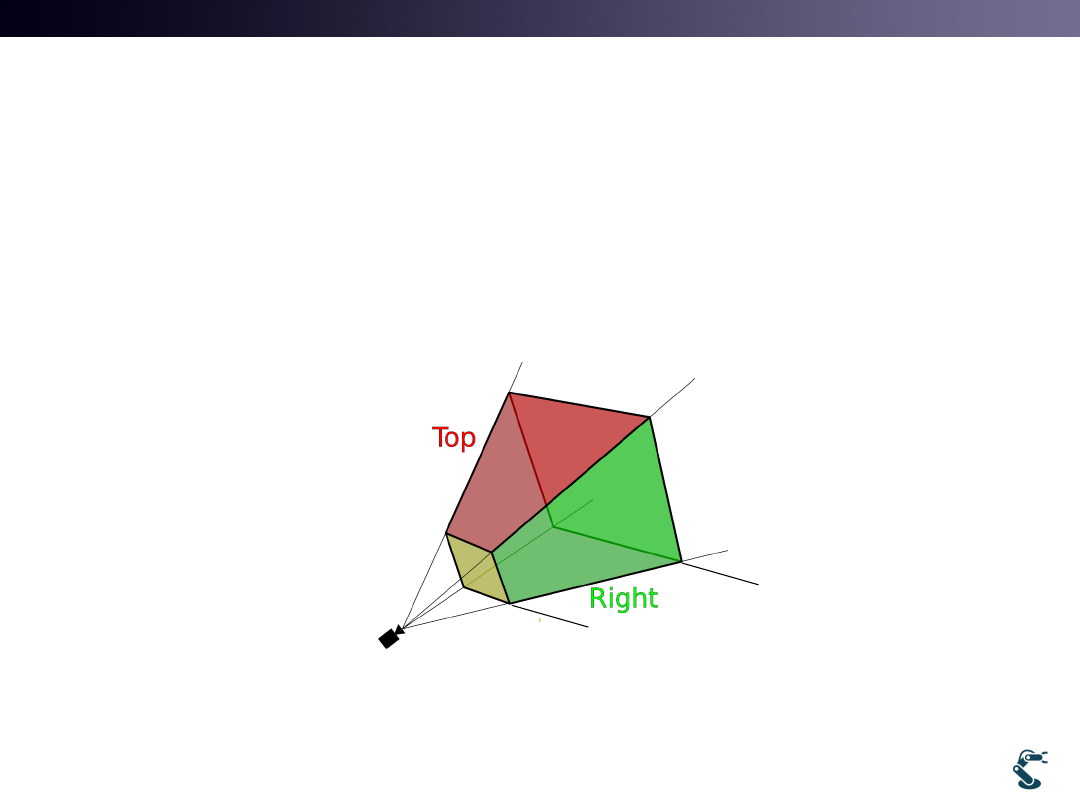
Basic Perspective View to Z axis
• Calculate P’(x’,y’,n) on near plane from P(x,y,z)
• Top of Pyramid is “Origin”, at which the Eye locates.15
3D Space
Near, n
Far, f
Z
X
z
x
y
Near,n
P(x, y, z)
z
x
'
( ,
0)
x
n
n
n
x
z
z
'
x
x
z
n
P’(x’, y’, n)
n
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Definition of Perspective Projection
• Perspective Projection
– Window size of near plane is l, r, t, b.
16
l
r
t
b
f
n

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
1. Perspective Mapping
• Recall that
• Near plane : z= -1 ( n= -1)
• Map x to and map y to
17
3D Space
Unit Space
W=H=T=[-1,1]
Near
Far
Near
Far
x
z
y
z
'
. 13
x
x
z
pp
z
Objects in the Frustum are mapped into the unit space

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Derivation of Perspective Mapping
(Original Derivation)
18
'
0
0
0
'
0
0
0
'
0
0
1
0
0
1
1
ex
bz
d
x
e
x
ex
fy
y
f
y
fy
bz
d
z
a
c
z
az
c
az
c
b
d
bz
d
bz
d
To map to '
(
0),
x
x
x
z
z
1,
1,
0
ex
e
b
d
bz
d
To map to '
(
0),
y
y
y
z
z
1,
1,
0
fy
f
b
d
bz
d
'
az
c
az
c
z
bz
d
z
, , , , ,
?
a b c d e f

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Derivation of Perspective Mapping
(Short Derivation)
19
'
1
0
0
0
'
0
1
0
0
'
0
0
1
0
0
1
1
x
bz
d
x
x
x
y
y
y
y
bz
d
z
a
c
z
az
c
az
c
b
d
bz
d
bz
d
To map to '
,
x
x
x
z
1,
0
x
b
d
bz
d
To map to '
,
y
y
y
z
1,
0
y
b
d
bz
d
'
az
c
az
c
z
bz
d
z
, , ,
?
a b c d

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Think Z in Near Plane and Far plane
20
'
(z<0)
az
c
az
c
z
bz
d
z
, then '
1
'
1
if z
n
z
an c
z
n
an c
n
, then ' 1
' 1
if z
f
z
af
c
z
f
f
af
c
f
af
n
an
n
f
a
n
f
(
1)
2
1
c
a
n
n
f
nf
c
n
n
f
n
f
,
0
if n f

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Perspective Matrix
21
1
0
0
0
'
1
0
0
0
0
1
0
0
'
0
1
0
0
2
0
0
'
0
0
1
0
0
1
1
0
0
1
0
x
x
x
y
y
y
n
f
nf
z
a
c
z
z
n
f
n
f
b
d
1
0
0
0
0
1
0
0
2
0
0
0
0
1
0
Perspective Matrix
n
f
nf
n
f
n
f

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Normalization
of Perspective Matrix Result
22
1
0
0
0
'
0
1
0
0
'
2
2
0
0
'
1
1
0
0
1
0
(
)
2
1
(
0)
(
)
T
x
x
x
y
y
y
n
f
nf
n
f
nf
z
z
z
n
f
n
f
n
f
n
f
z
x
y
z n
f
nf
z
z
z
z n
f
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
See uWnd-19-3D-Perspective-Projection
• uObj::Draw line 39
23
1
0
0
0
'
0
1
0
0
'
(
0)
2
2
0
0
'
1
1
0
0
1
0
x
x
x
y
y
y
z
n
f
nf
n
f
nf
z
z
z
n
f
n
f
n
f
n
f
z
(
)
2
1
(
0)
(
)
T
x
y
z n
f
nf
z
z
z
z n
f
ˆ
ˆ
'
x
Px
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
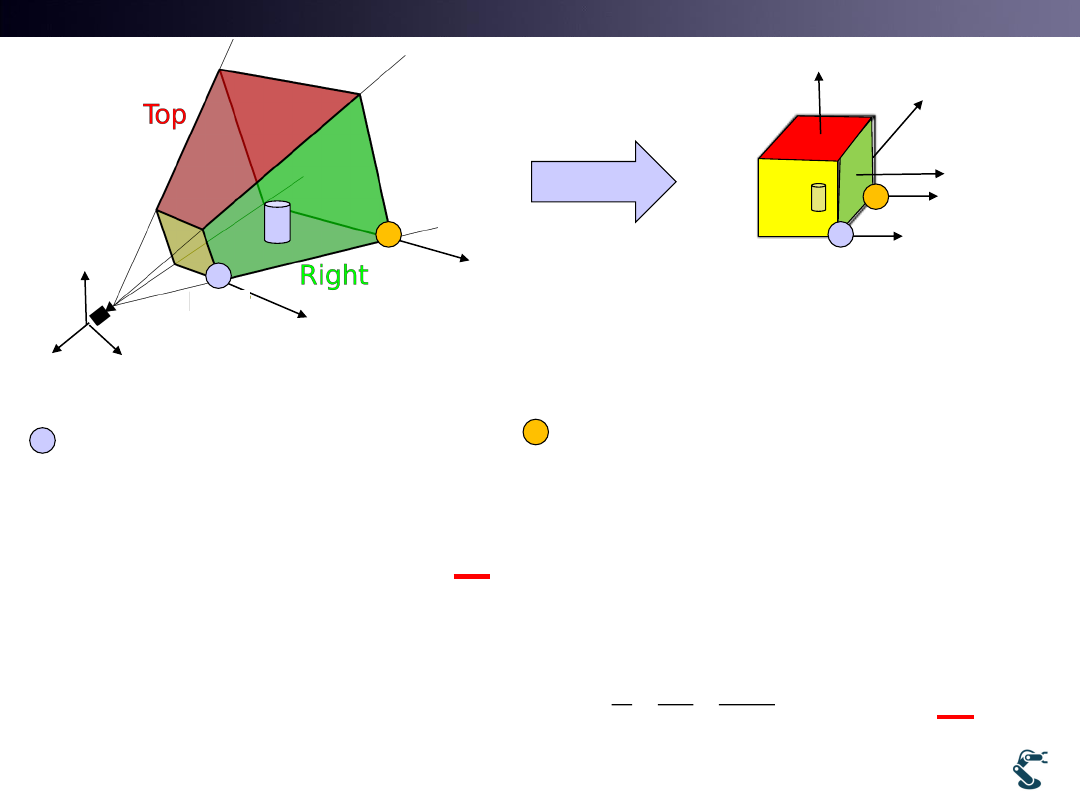
Example 1.
Calculation of Perspective Projection Mapping
24
1
0
0
0
0
1
0
0
2
0
0
0
0
1
0
P
n
f
nf
n
f
n
f
,
0
n f
3D Space
Unit Space
W=H=T=[-1,1]
Near
Far
Near
Far
z
that
1
65535
Assume
n
f
1
0
0
0
0
1
0
0
0
0
1
2
0
0
1
0
P
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
25
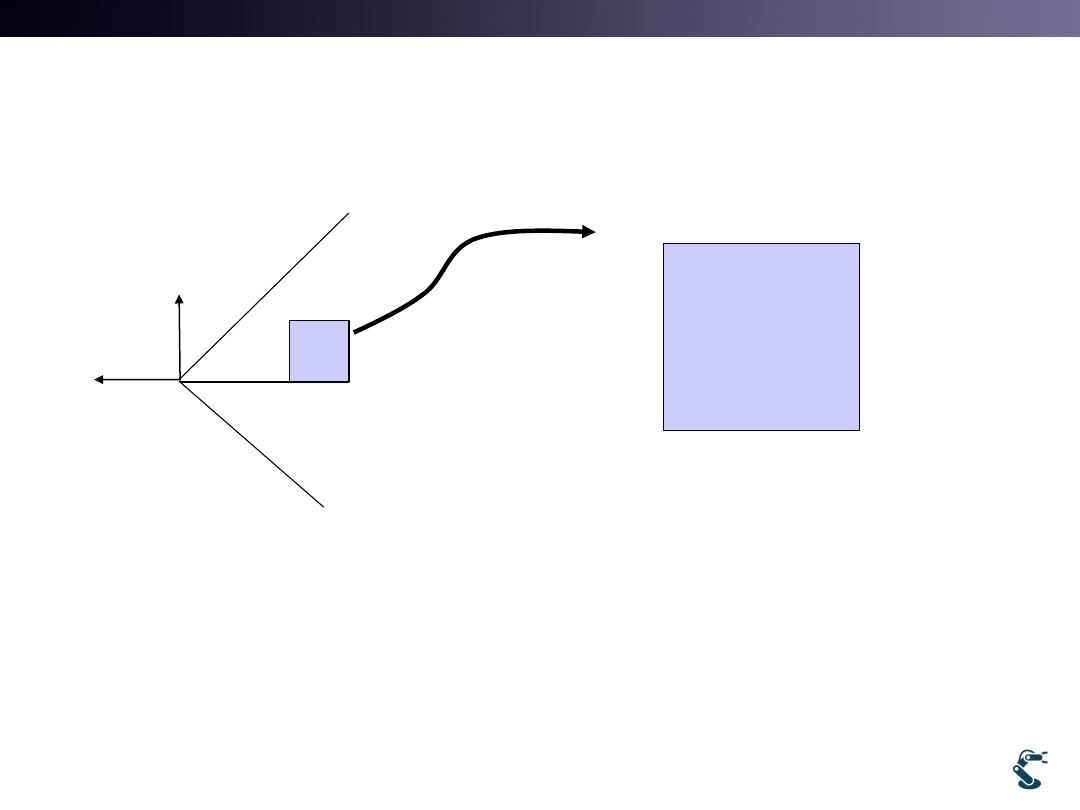
3D Space
Unit Space
W=H=T=[-1,1]
Near
Far
Near
Far
z
1, 1, 1,1
1
0
0
0
1
1
0
1
0
0
1
1
0
0
1
2
1
1
0
0
1
0
1
1
T
X
X
PX
65535, 65535, 65535,1
( ,
,
,1)
1
0
0
0
0
1
0
0
0
0
1
2
2
0
0
1
0
1
2
1
1
1 1 1
T
T
T
T
X
f
f
f
f
f
f
f
f
f
f
X
PX
f
f
f
f
f
f
z
x
y
x
y
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
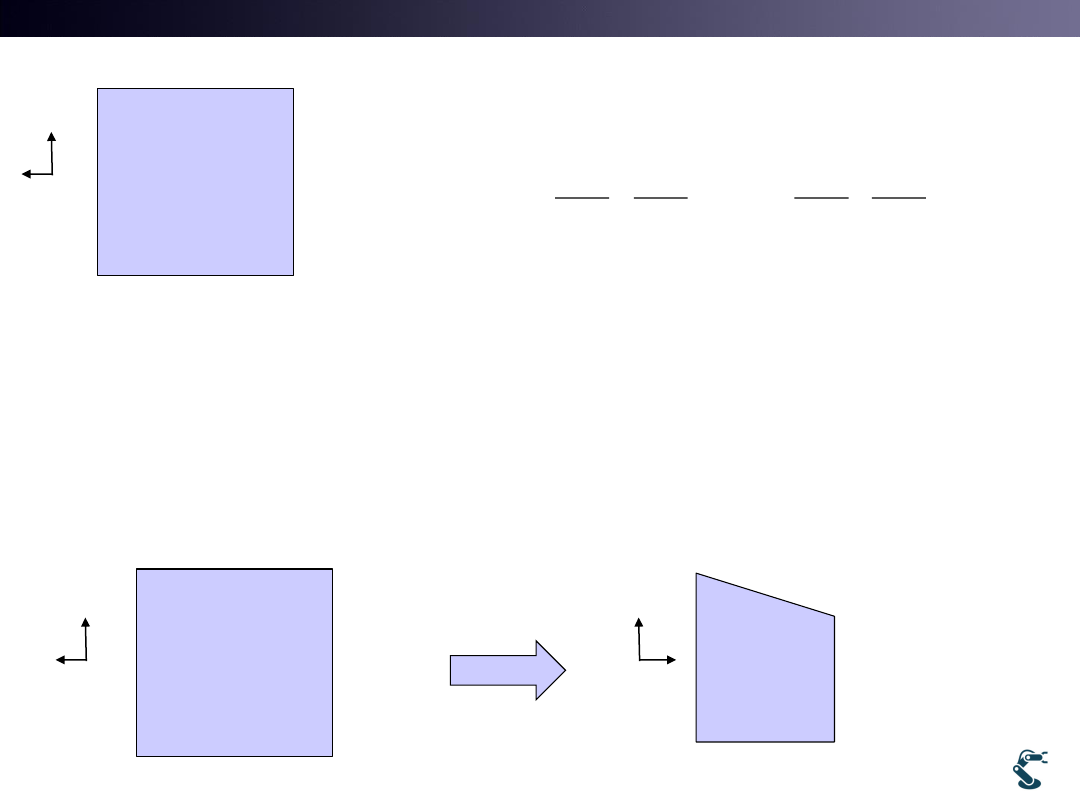
Example 2.
From 3D to 2D
26
z
y
3d
3d
(0,0,-2)
(0,0,-3)
(0,1,-2)
(0,1,-3)
1
0
0
0
0
1
0
0
0
0
1
2
0
0
1
0
P
0 1
2 1
0 1 0
2
0
0
2 1
0
0
0
2
0 1
3 1
0 1 1 3
0
0
3 1
0
0 1 3
T
T
T
T
T
T
T
T
P
P
P
P
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
27
(0,0,-2)
(0,0,-3)
(0,1,-2)
(0,1,-3)
0 1
2 1
0 1 0
2
0
0.5
0 1
(
-2
0)
0
0
2 1
0
0
0
2
0
0
0 1
(
-2
0)
0 1
3 1
0 1 1 3
0
0.33 0.33 1
(
-3
0)
0
0
3 1
0
0 1 3
0
0
0.33 1
(
-3
0)
T
T
T
T
T
T
T
T
T
T
T
T
P
z
P
z
P
z
P
z
.23
1
0
0
0
'
0
1
0
0
'
(
0)
2
2
0
0
'
1
1
0
0
1
0
pp
x
x
x
y
y
y
z
n
f
nf
n
f
nf
z
z
z
n
f
n
f
n
f
n
f
z
(0,0,-2)
(0,0,-3)
(0,1,-2)
(0,1,-3)
(0,0,0)
(0,0.5,0)
(0,0.33,0.33)
(0,0,0.33)
z
y
z
z
y

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
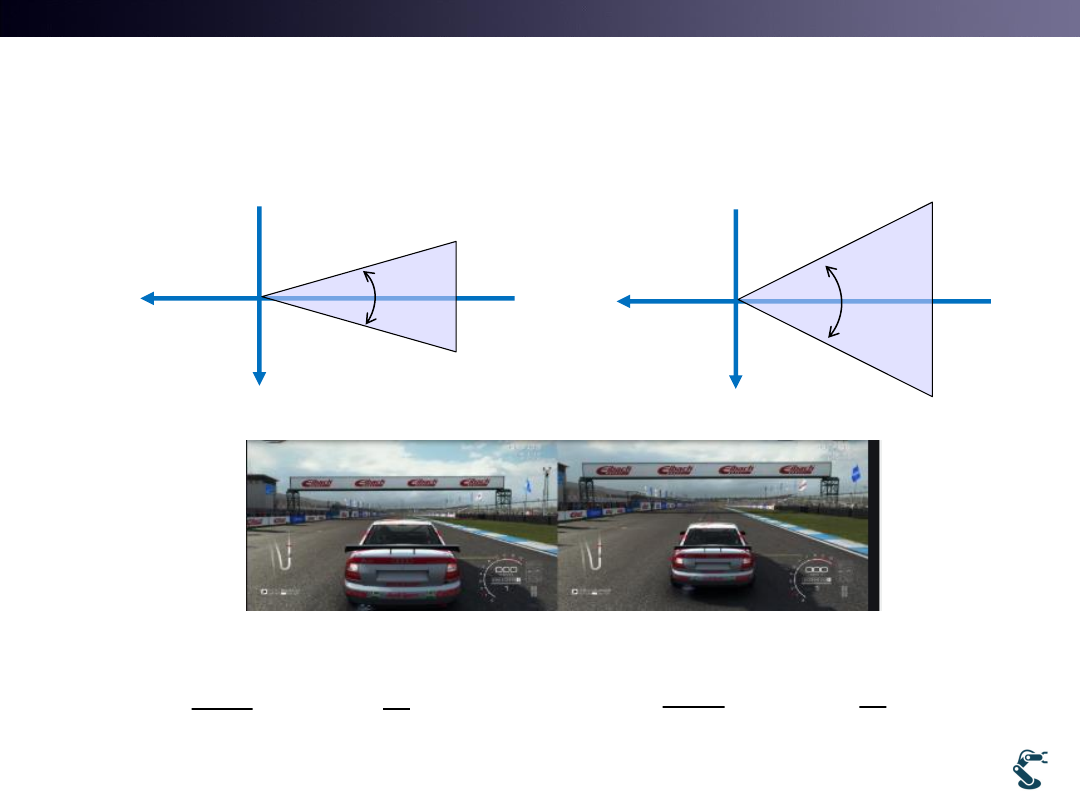
2. Aspect Ratio
• Aspect ratio = width/height
– Ex) AR = 1366/768
28
w
h
It is NOT a Square!
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
3. Field of View (FOV)
29
Z
X
Z
X
'
cot
2
n
x
x
x
r
l
'
cot
2
n
y
y
y
t
b
n
n

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
4. Aspect Ratio and FOV are applied
• This matrix is same with gluPerspective in OpenGL
– n = 1 and f=65535
• Keep in mind gluPerspective is deprecated in
OpenGL ES.
30
cot( / 2)
0
0
0
/
0
cot( / 2)
0
0
2
0
0
0
0
1
0
W H
P
n
f
nf
n
f
n
f
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Special Cases:
Condition that Frustum is Skewed,
Shearing and Clipping are Needed.
31
L
R
l
r
What
Are you
looking at?
• Skewed projection becomes Popular in VR.
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
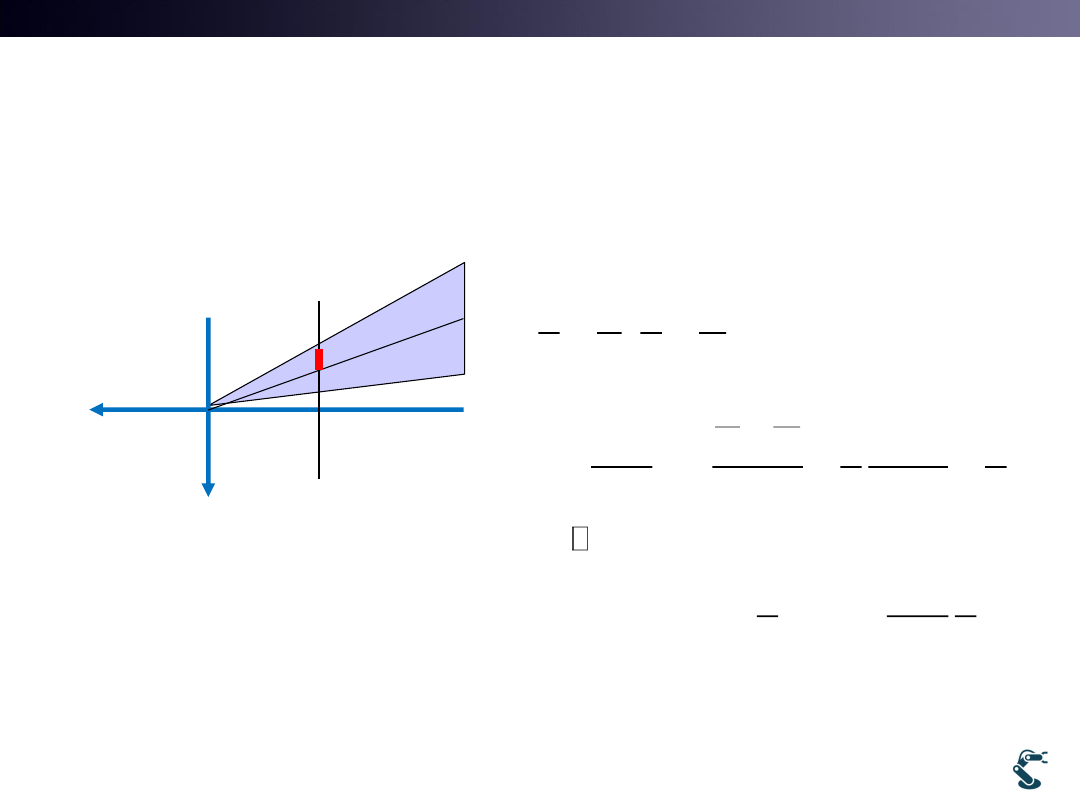
5. Shearing Window to Z axis
32
Z
X
n
L
R
l
r
,
2
2
2
'
|
|
'
x
2
l
L r
R
n
z n
z
L
R
l
r
n L
R
n
z
z
o
n
O
z
z
x
x
O
z
l
r z
x
x O
o
x
n
n
O
o
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
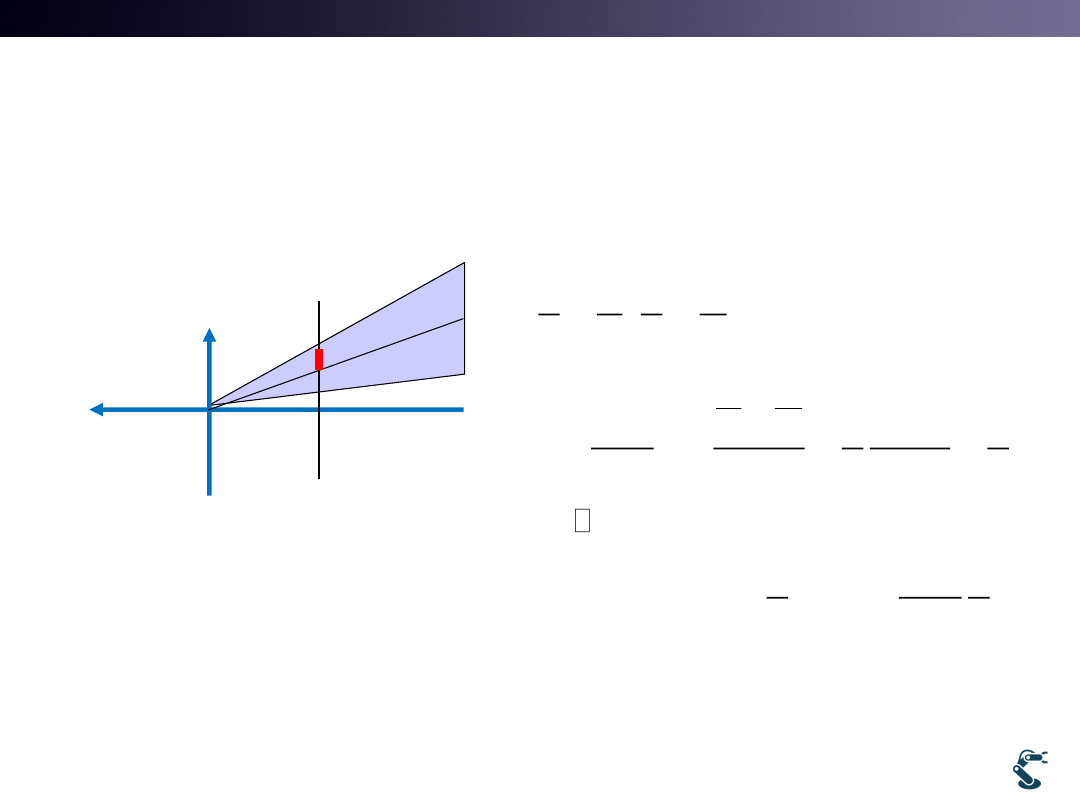
5. Shearing Window to Z axis
33
Z
y
n
T
B
t
b
,
2
2
2
'
|
|
'
2
t
T b
B
n
z n
z
T
B
t
b
n T
B
n
z
z
o
n
O
z
z
y
y
O
z
t
b z
y
y
O
y
o
y
n
n
O
o

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
5. Shearing Window Matrix
• Shearing Window Matrix in Homogeneous Transform
34
'
2
'
2
'
x
x
y
y
z
l
r z
x
x O
x
o
x
n
n
z
t
b z
y
y
O
y
o
y
n
n
z
z
1
0
0
'
2
'
0
1
0
2
'
0
0
1
0
1
1
0
0
0
1
l
r
x
x
n
y
t
b
y
n
z
z
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
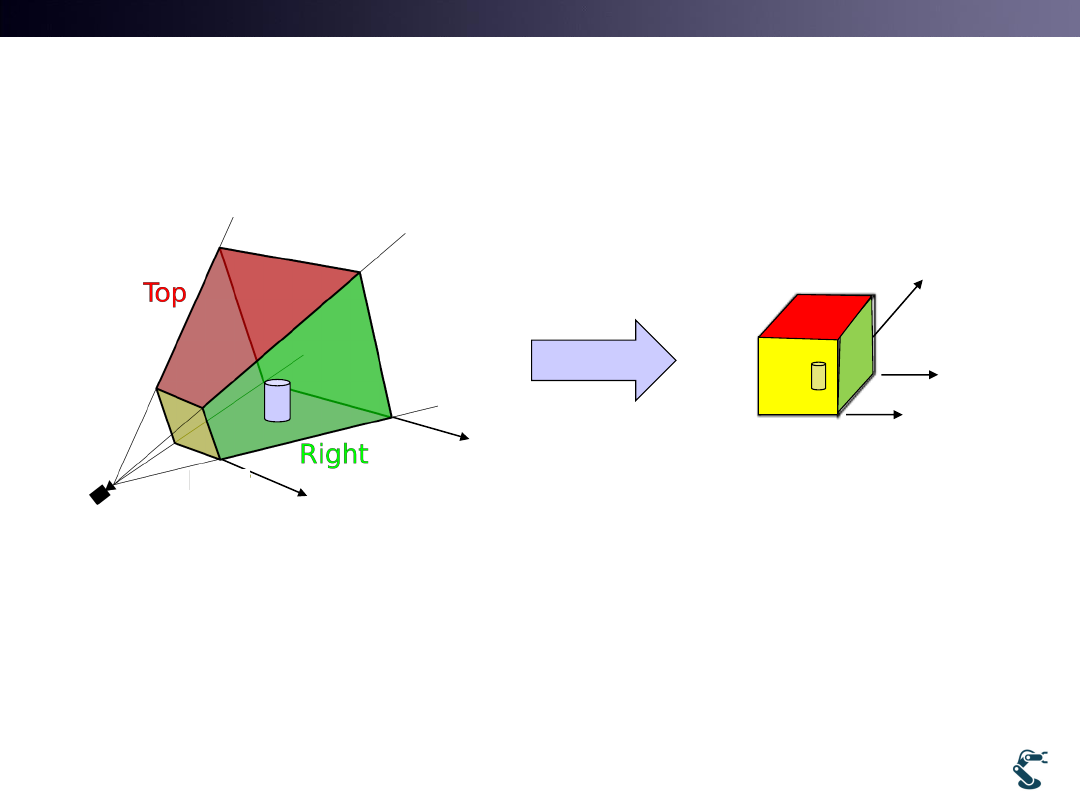
6. Clipping Boundaries
• Clipping object and Mapping intro Unit space
– Width=[-1,1]
– Height=[-1,1]
– Thickness=[-1,1]
35
3D Space
Unit Space
W=H=T=2
Near
Far
Near
Far
z

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
6. Clipping Boundaries
• Think plane
36
3D Space
Near, n
Far, f
z
x
y
y
z
y
z
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
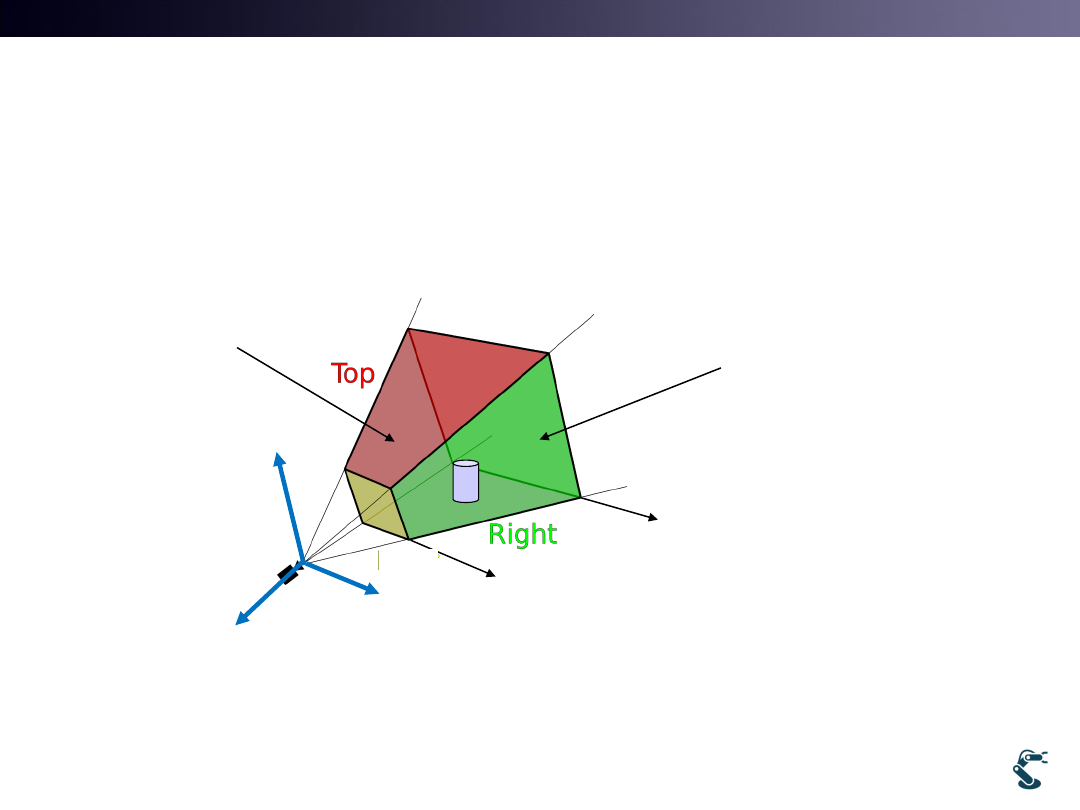
6. Clipping Boundaries
• Think plane
37
3D Space
Near, n
Far, f
z
x
y
x
z
x
z
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
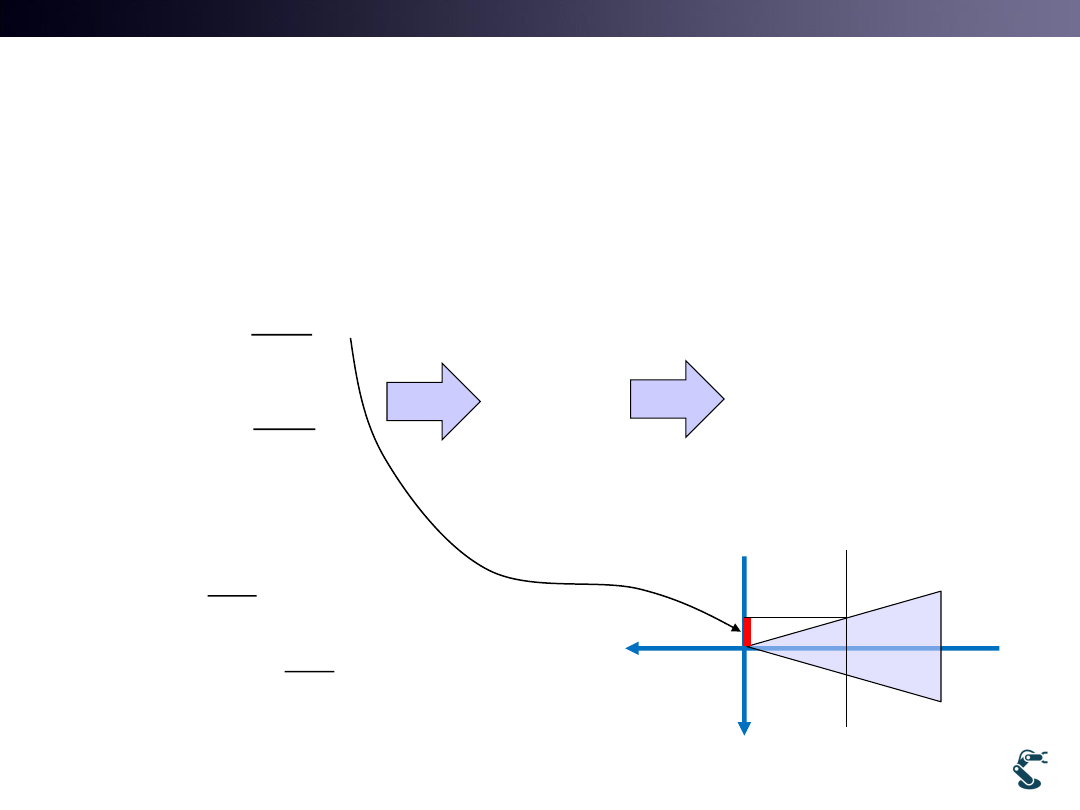
6. Clipping Boundaries
• Clipping boundaries into Unit Space [-1,1]
38
2
'
2
'
'
n
x
x
r
l
n
y
y
t
b
z
z
1
1
1
1
1
r
l
t
b
n
'
'
'
x
x
y
y
z
z
2
0
0
0
'
'
2
0
0
0
'
0
0
1
0
1
1
0
0
0
1
n
x
x
r
l
y
n
y
t
b
z
z
Z
X
n
l
r
x’

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
7. Skewed Perspective Projection matrix
39
2
1
0
0
0
0
0
0
1
0
0
2
0
1
0
0
2
0
0
0
0
1
0
2
2
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
1
2
0
0
2
0
0
2
0
0
P
Perspective Clipping Shearing
n
l
r
r
l
n
n
t
b
n
f
nf
t
b
n
n
f
n
f
n
r
l
r
l
r
l
n
t
b
t
b
t
b
n
f
nf
n
f
n
f
0
0
1
0
1
1
1
1
1
r
l
t
b
n
1
0
0
0
0
1
0
0
2
0
0
0
0
1
0
n
f
nf
n
f
n
f
Skewed Perspective Projection
Perspective Projection
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
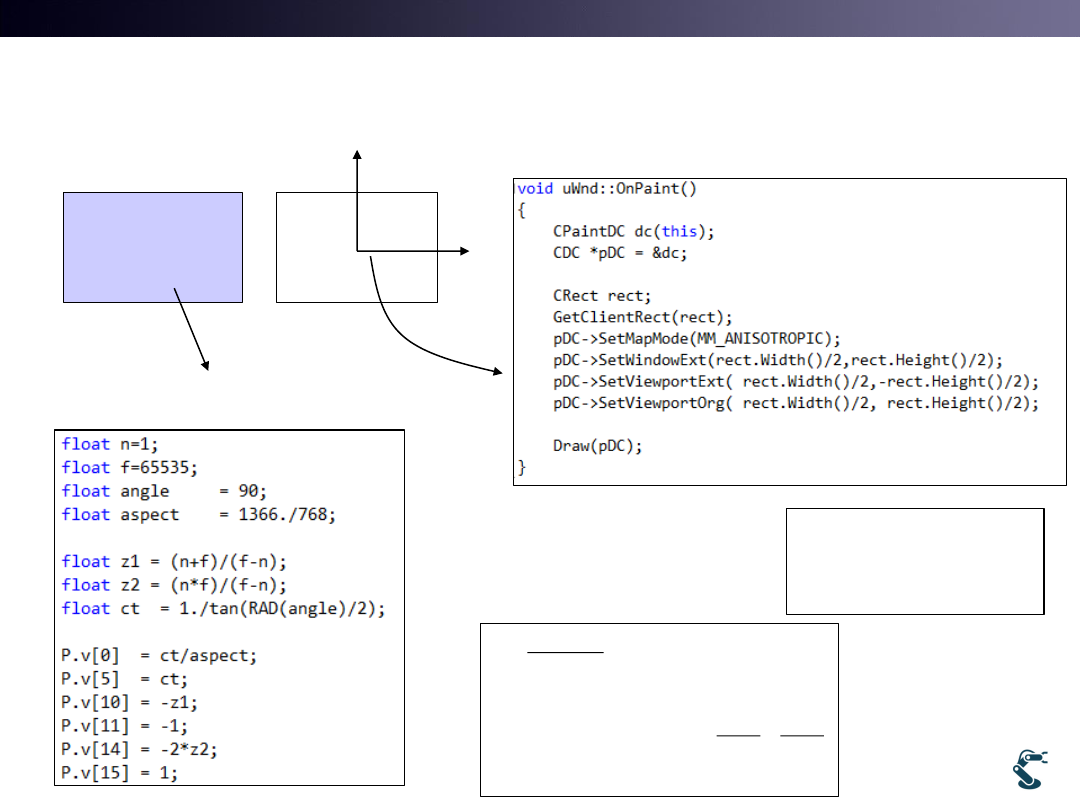
Ex) uWnd-19-3D-Perspective-Projection
40
uWnd
X
Y
hMat P : Perspective Projection
v[0]
v[4]
v[8]
v[12]
v[1]
v[5]
v[9]
v[13]
v[2]
v[6]
v[10]
v[14]
v[3]
v[7]
v[11]
v[15]
hMat
cot( / 2)
0
0
0
/
0
cot( / 2)
0
0
2
0
0
0
0
1
0
W H
P
n
f
nf
n
f
n
f
pp. 23
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
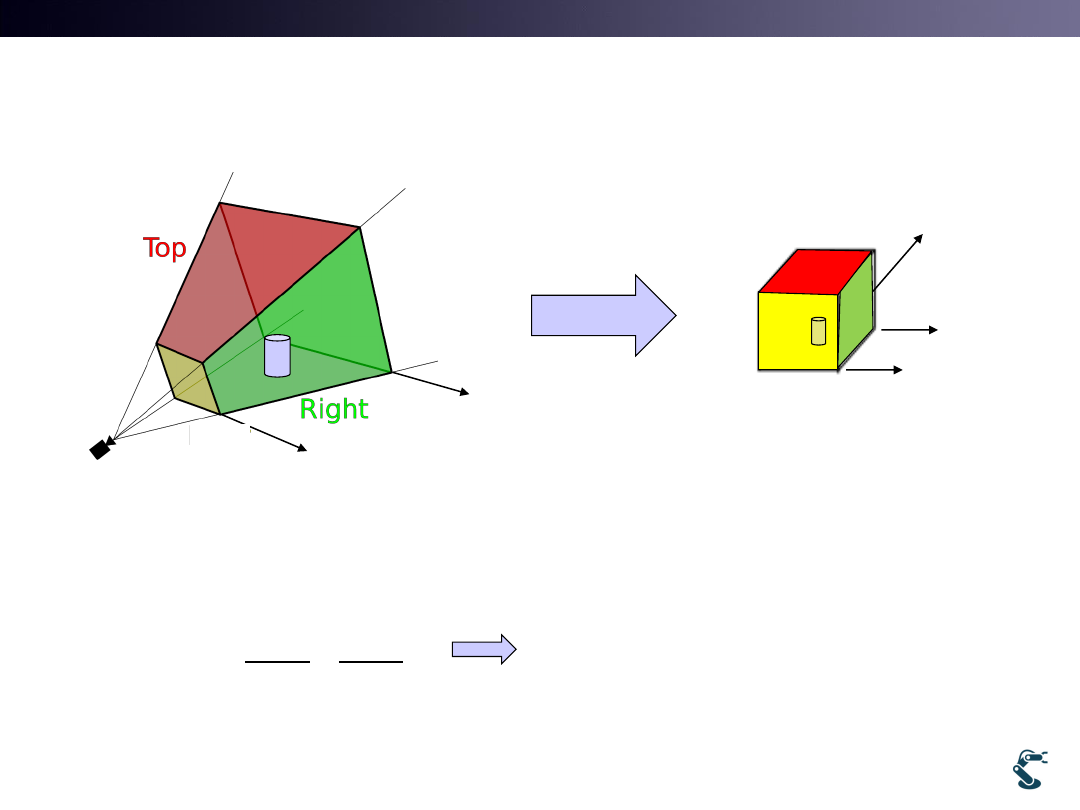
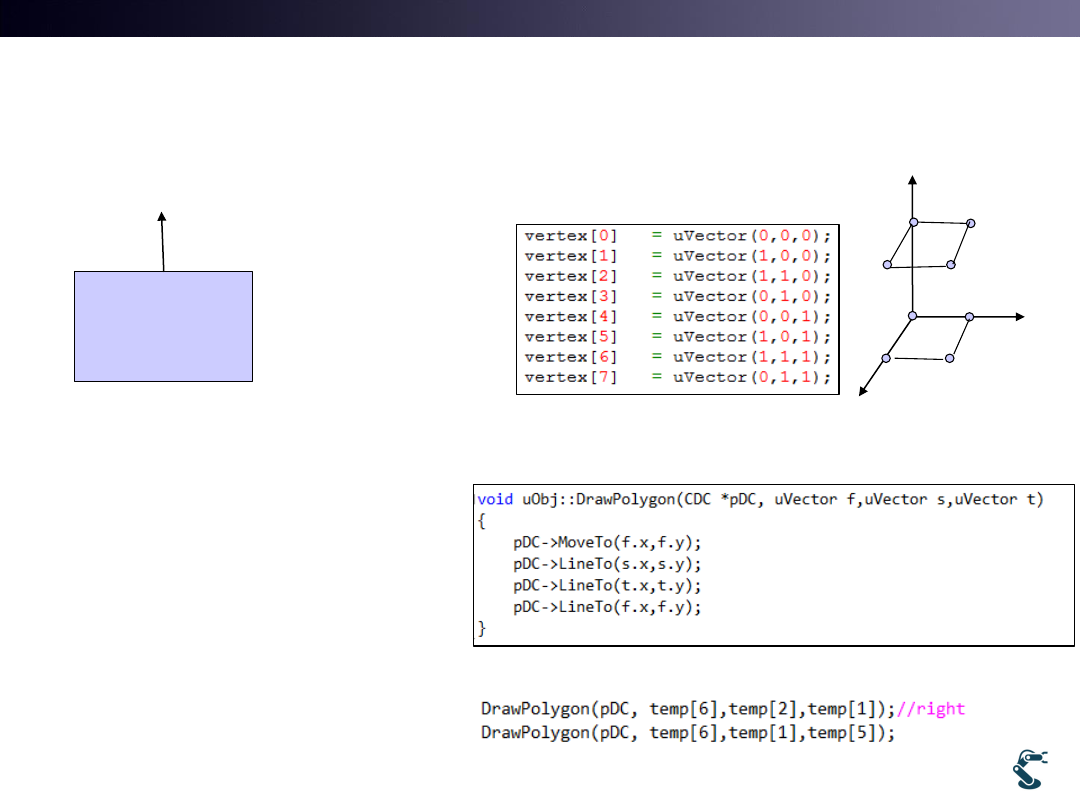
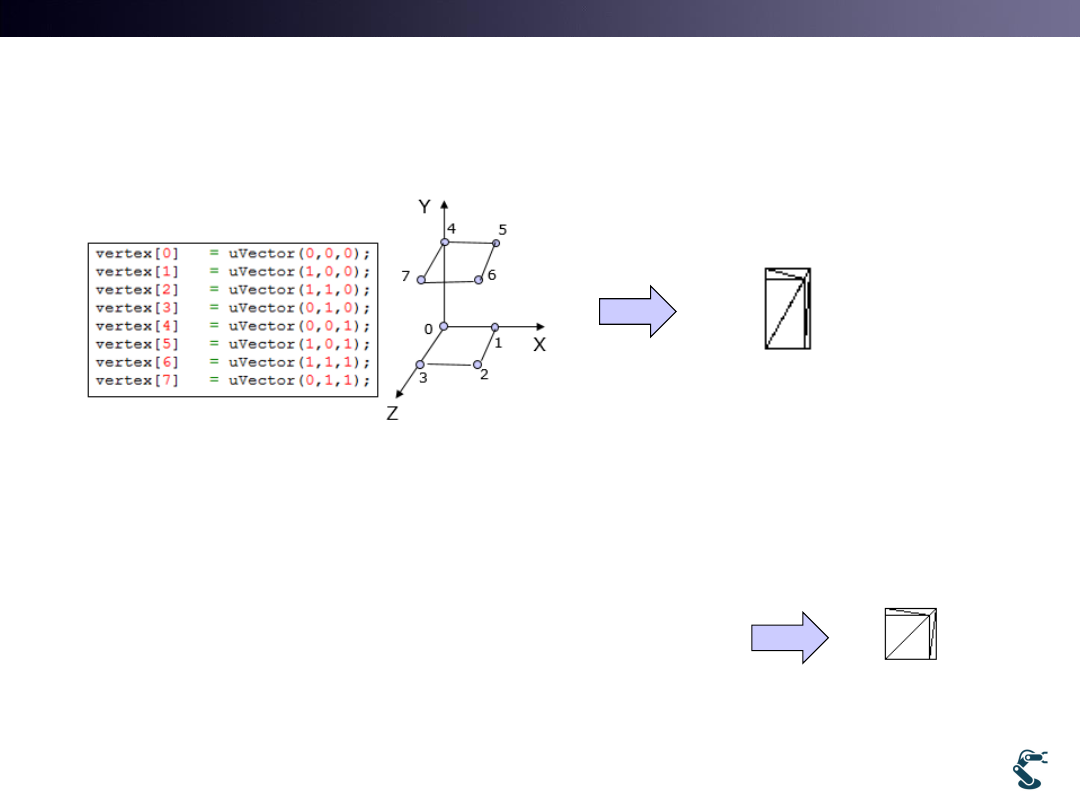
3D Object Building
41
uObj
X
Y
Z
0
1
2
3
6
4
5
7
hMat H, P, S
H: Object transform
P: Perspective
Projection
S: Scaling
Polygon with 3 vertices
Draw Counter Clock Wise
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
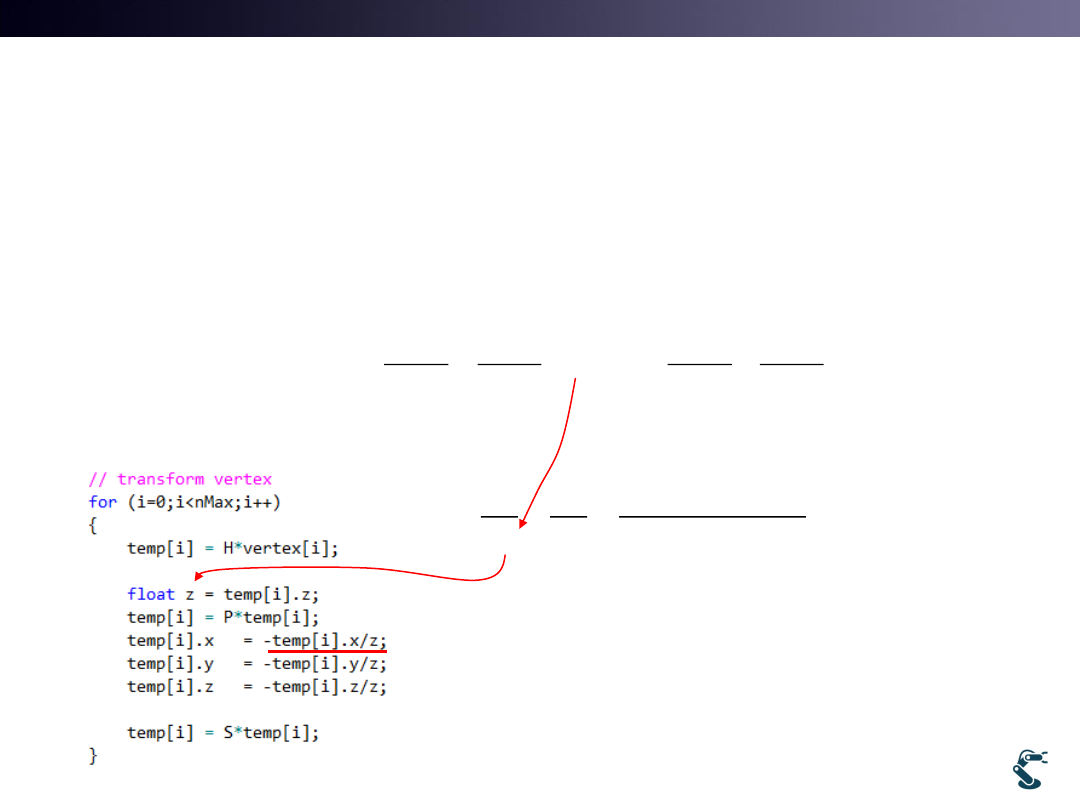
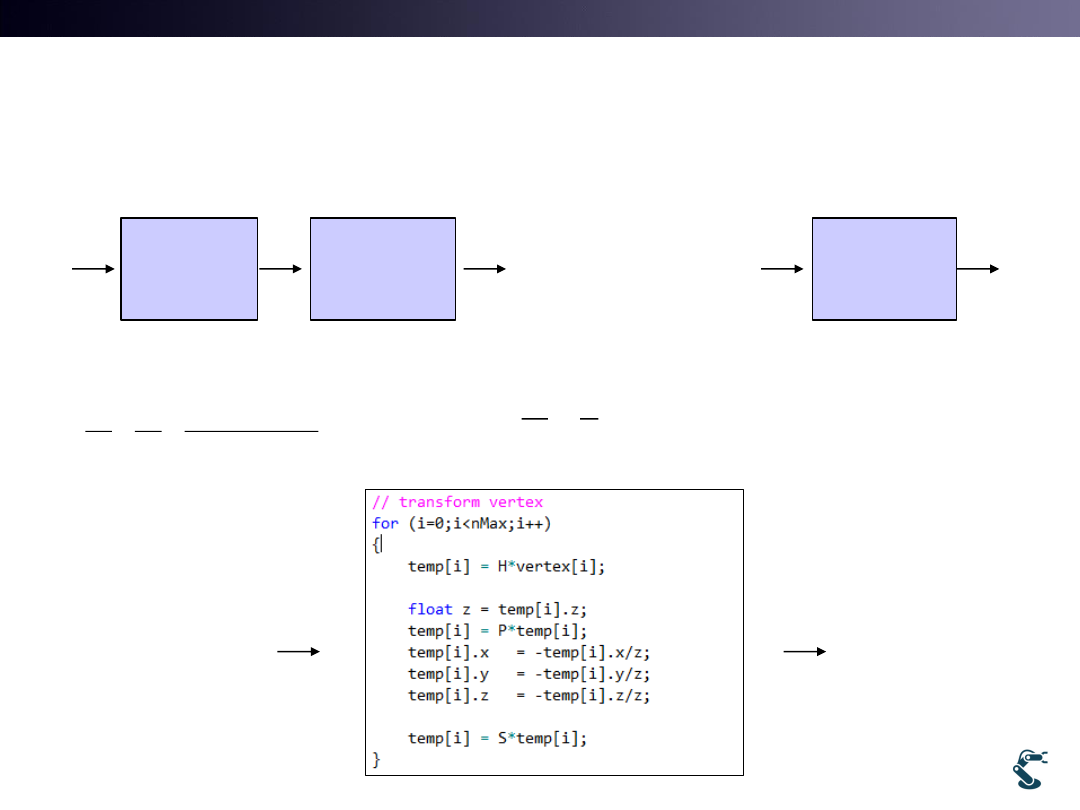
Drawing with Perspective Projection
42
uObj::H
x
y
z
vertex
/ z
'
/ z
'
1
'
x
x
x
y
y
y
z
z
uObj::P
Perspective
Projection
Remind
'
x
n
x
z
uObj::S
Scale
', y' [ 1,1]
x
', y'
640 x 480
x
x
y
z
3D
vertex
'
'
1
x
y
2D
temp
(
)
2
'
1
(
0)
(
)
T
x
y
z n
f
nf
X
z
z
z
z n
f

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
43
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
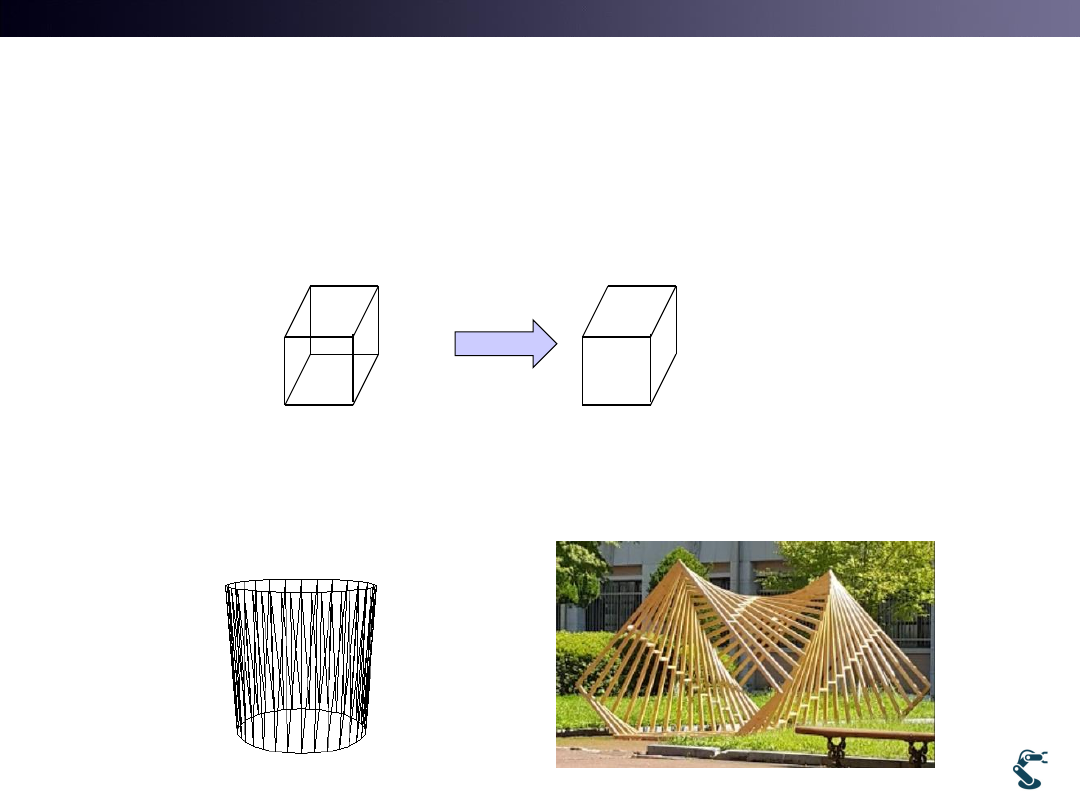
Why Width and Height are Different?
• Answer: That is aspect ratio.
• Windows CDC already changes aspect ratio
• Thus, modify aspect ratio=1
44
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
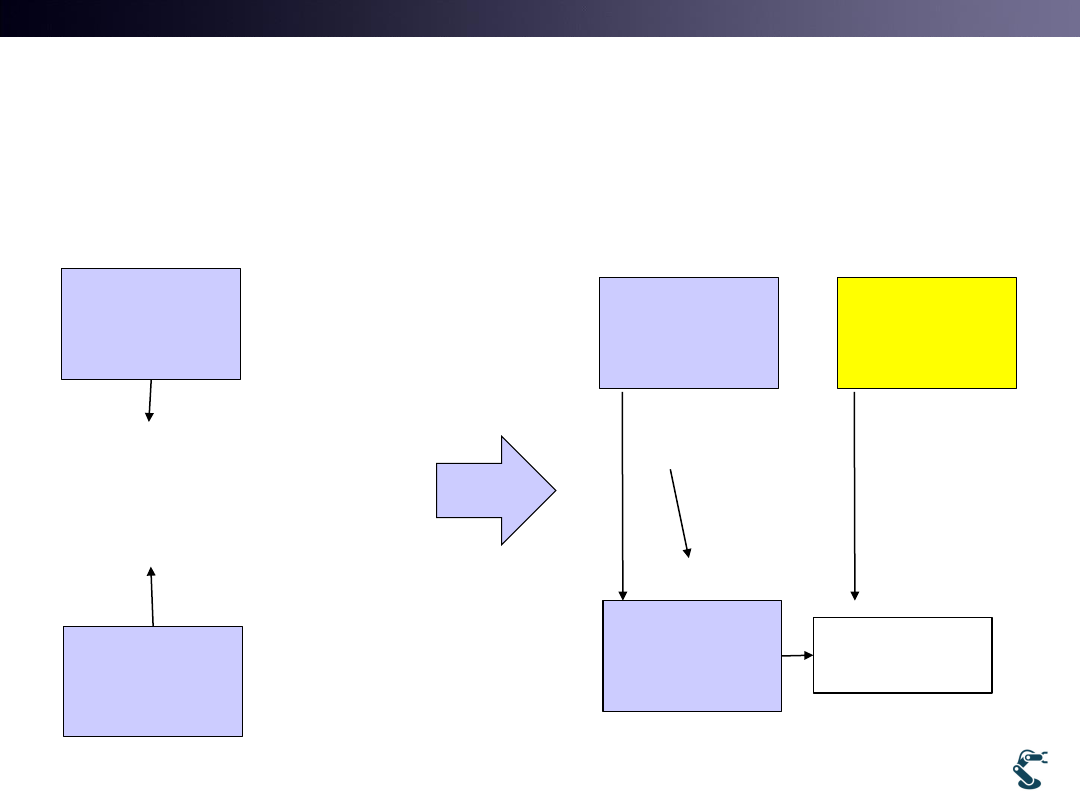
Ex) uWnd-20-3D-PP-Camera
New Class: uCam for projection
• Think, this structure is somewhat bad.
45
uWnd
hMat P : Perspective Projection
uObj
hMat H, P, S
uWnd
uCam
(Viewpoint)
uObj
hMat H
hMat P,S
Run()
Draw()
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Next week
• Hidden surface removal
• Various types of Objects
46