
5
장 자계(磁界)
5.1
자석
5.2
자기유도
5.3
자기모멘트
5.4
자화의세기
5.5
자계
5.6
자위
5.7
정전계와 정자계의 비교

5.1
자석(magnet, 磁石)
◈ 고대 그리스의 magnetitte 지역에서 발견된 광석으로
지역이름을 도용해서 magnet 라 함)
S
자석은 항상 N 극과 S 극이 함께 존재
N
극만 있다던가 혹은 S극만 있는 경우는 없음.
S
S
자석을 둘로 자르면, 둘다 자석이 됨.
S
S
S
S
N
같은 극 끼리는 척력이 작용
다른 극끼리는 인력이 작용
S
N
N
S
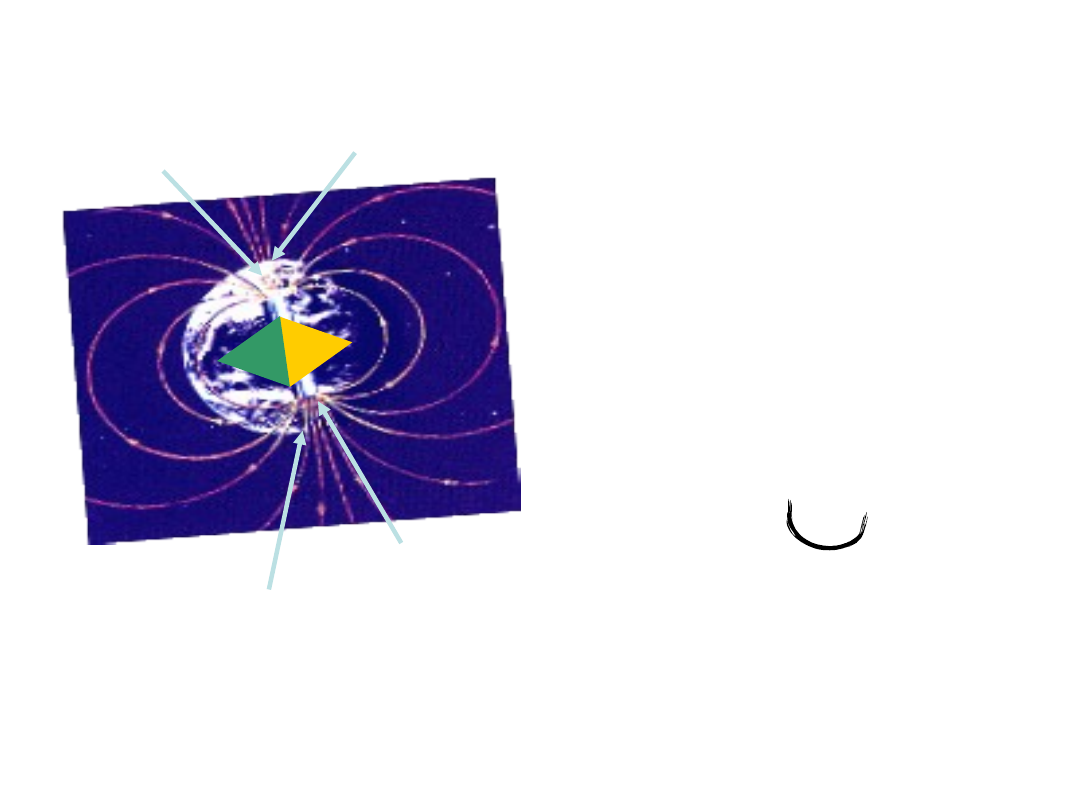
지자기 북극
지리학적 북극
지리학적 남극
지구는 거대한 자석이다.
지자기의 근원; 자기장은 전하를 띤
물체가 운동을 할 때 발생한다. 전하를
운반하는 지구 핵의 대류에 의해
발생한다. 즉 지구 내부에 자리잡은
액체에 있는 전하를 띤 물체 혹은
전자의 회전에 의해 발생한다.
N
S
지자기 남극
◈ 지자기 --> 지구는 자석이란 뜻

◈ 오로라
(aurora)
오로라는 라틴어에서‘새벽’이란 뜻으로 1621년 프랑스의 과학자 피에르 가센디가
로마신화 등장하는 여명의 신 `아우로라(Aurora, 그리스 신화의 에오스)를 따서
이름을 붙였다.
►
오로라는 태양 표면에서 날아온 전기를 띤 입자가 지구자계와 상호 작용에 의해
극지방 상층 대기에서 일어나는 대규모 방전현상이라고 할 수 있다.
►
지구는 거대한 자석으로 남북으로 자기장을 만든다. 태양은 항상 양성자와 전자로
이루어진 대전 입자를 방출하고 있다. 오로라를 일으키는 재료인 대전 입자는
태양으로부터 공급된다. 태양에서는 빛 외에도 전기를 띤 많은 입자를 쏟아내는데,
이 입자들의 흐름을 바람에 비유하여 “태양풍” 이라고 한다.
태양풍은 1cm3당 1~10개의 입자를 가지고 있으며, 평균 속도 500km/s에 달한다.
►
지구에 도달하는 대부분의 태양풍은 지구의 자기장 밖으로 흩어지고, 일부는 지구의
자기권에 끌려들어 자기의 북극과 남쪽으로 지구 대기로 하강한다.
►
하강한 대전입자는 고도 100~500km 상공에서 대기와 충돌하면서 기체(원자와
분자)를 이온화하는 과정에서 가시광선과 자외선 및 적외선 영역의 빛을 내는데,
우리는 가시광선 영역의 오로라를 보게 된다.
태양의 활동이 활발해지면 태양풍이 강해져서 오로라에 의해 통신장애가 발생.

5.2
자기유도(magnet, induction)
•
자기유도란 자석의 성질, 즉 N극과 S극을 유도시킨다는 뜻으로 자화(磁化)라고도 함.
N
S
S
N
S
N
S
N
N
S
N
S
N
S
•
자화되지 않은 물질을 자석에 가까이 대면
그림과 같이 자석의 특성이 나타나는데,
이를 자기유도 혹은 자화(磁化)라고도 함.
►
자기유도는 물질의 특성에 의해 다음의 3 종류로 분류됨.
①
상자성체 ②
반자성체 ③ 강자성체

① 상자성체 ( 常磁性體 paramagnetic material) ; 다른 극이 유도되는 물질
예) 백금(Pt), 알루미늄(Al)
② 반자성체 ( 反磁性體; diamagnetic material) ; 같은 극이 유도되는 물질
예) 은(Ag), 구리(Cu), 금(Au), 인(P)
③ 강자성체 ( 强磁性體; ferromagnetic material) ; 자화된 뒤에 자석을 멀리
떠어뜨려도 자성이 지속되는 물질 예) 철(Fe), 니켈(Ni), 코발트(Co), 망간(Mn)
N
S
N
S
상자성체
N
S
S
N
반자성체

◈ 분자는 자성을 가진다
. 이를 자기분자 혹은 분자자석 이라고 표현한다.
► 분자는 물질의 최소 단위. 따라서 분자자석은 자석의 최소 단위가 된다.
► 분자 자석을 간단히 나타내면,
•
•
분자
S
N
원자
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
NS
N
S
N
S
N
S
N
S
N
S
N
S
N
평상시에 물질내부의 분자들은 임의로
분포하기 때문에 물질은 자화되어 있지
않다. 즉 각각의 분자자석에서 방출하는
자계가 임의의 방향으로 분포되므로
평군하면 0이 된다.
자석을 가까이 가져가면 물질내부의
분자들은 자석의 방향으로 일렬로
정돈한다. 모든 분자자석들이 동일한
방향으로 자계를 방출한다. 물질은
자화된다. 상기 예는 상자성체임.
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
NS
N
S
N
S
N
S
N
S
N
S
N
S
N
N
S
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
상자성체
반자성체
강자성체
자석을 치우면, 물질내부의 분자들은
임의로 분포하기 때문에 자화되지
않는다. 그러나 강자성체는 오랫동안
자화되어 있다.
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
S
N
◈ 자기 쌍극자 (magnetic dipole)
물질의 자화 세기는, 물질을 구성하는 분자들의 자화 세기에 비례한다.
아래에 분자의 자기량을 +m 과 –m 으로 표시하자.
•
•
분자
S
N
+m
–m
m
은 대단히 작은 양이고, 원자 간의 거리 l 도 매우 작기 때문에
마치 +m과 –m의 자극이 한 점에 쌍을 지어 있는 것
처럼 보이기 때문에 이를 자기쌍극자(magnetic dipol
e)
이라고 함.
+m
-m
l
+m
-m
l ≈ 10-6 cm
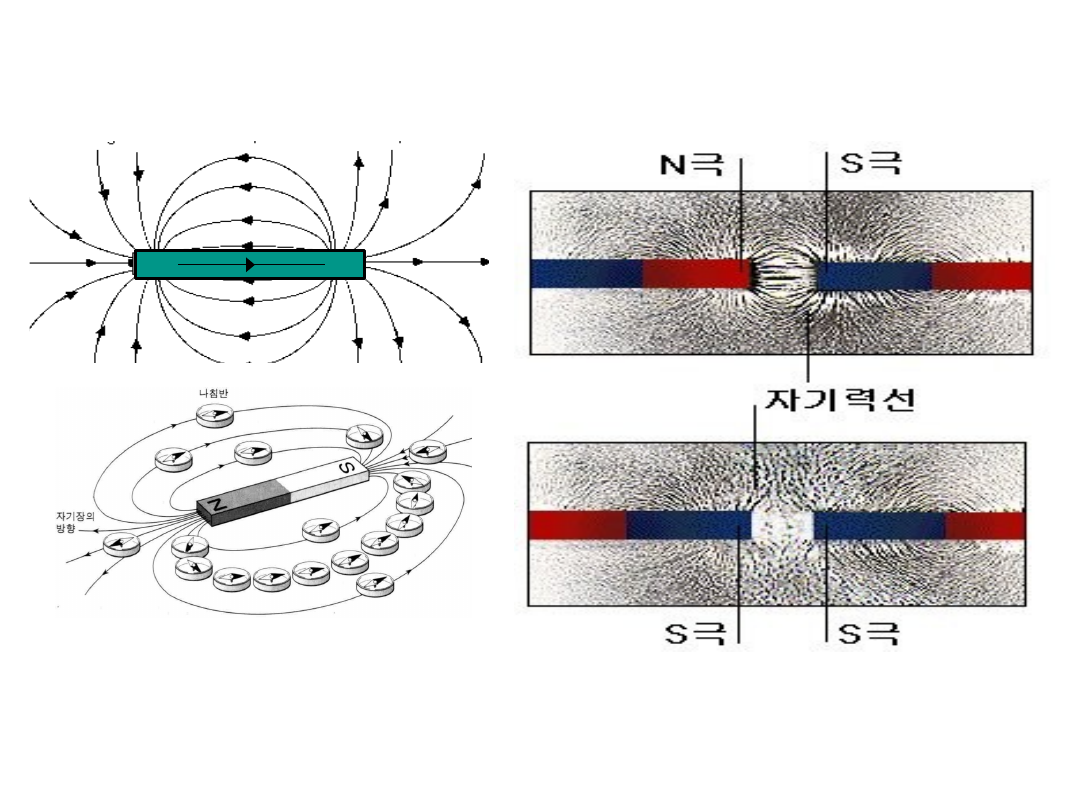
5.5
자계 (磁界)
5.5.1
자기력선(磁氣力線)
N
S
자석은 자계를 방출한다
자석은 자계를
. .
마치 전하가
마치
전계를 방출하는 것과 유사함
전계를 방출하는 것과
.
.
자계는 N
극에서 S
극으로 들어간다
극으로
5.5.2
자기력과 쿨롱의 법칙
자기량이 m
1, m2
인 두 물체가 직선거리 r
에 놓여 있을 때 이들 간에 작용하는
힘인 자력 F 는;
m
1
m
2
r
F = ·
r 2
m
1m2
1
= 0 · r로 정의한다. 0
;
진공에서의 투자율로 ,
0 = 4 10
-7
T·m/A
r비투자율(比透磁率), 진진진진진진진진진진진진진진진
진진진진진진진진진진진진진진진진
= 0 · r로 정의한다.
0 ;
진공에서의 유전율 값,
r비유전율로, 진진진진진진진진진진진진진진진

표 8.1 물질의 비투자율
구분
물질
비투자율
상자성체
진공
1
공기
1
알루미늄
1.000022
백금
1.000026
강자성체
철
5000
코발트
250
니켈
600
규소강
7000
78
퍼멀로이
100,000
반자성체
은
0.999974
구리
0.9999904
물
0.9999912
◈퍼멀로이 [Permalloy] 니켈과 철의 합금으로 철보다 더 높은 자기투과도를 나타내며 얇은
판으로 만들어 변압기 자심(磁心)에 주로 사용된다. 니켈의 비율은 용도에 따라 35~90%로
다양한데 저출력 변압기에는 78% 정도가 적당하다. 웨스팅하우스일렉트릭사의 상표명인
하이퍼닉은 니켈 함유율이 50%로 고출력변압기에 유용하다. 순수한 수소상태에서 5%의
몰리브덴을 함유한 퍼멀로이를 가열하면 훨씬 더 높은 자기투과도를 나타내는 슈퍼멀로이가
만들어진다

5.5.2
자기력과 쿨롱의 법칙
따라서 진공이나 공기중에서 자력 F는;
진진진진진
6 × 10-4 Wb진3 × 10-3 Wb진진진진진cm진진진진진진진진
진진진진진진진
F = ·
r 2
m
1m2
0
1
= 6.33 × 104
r 2
m
1m2
5.5.3
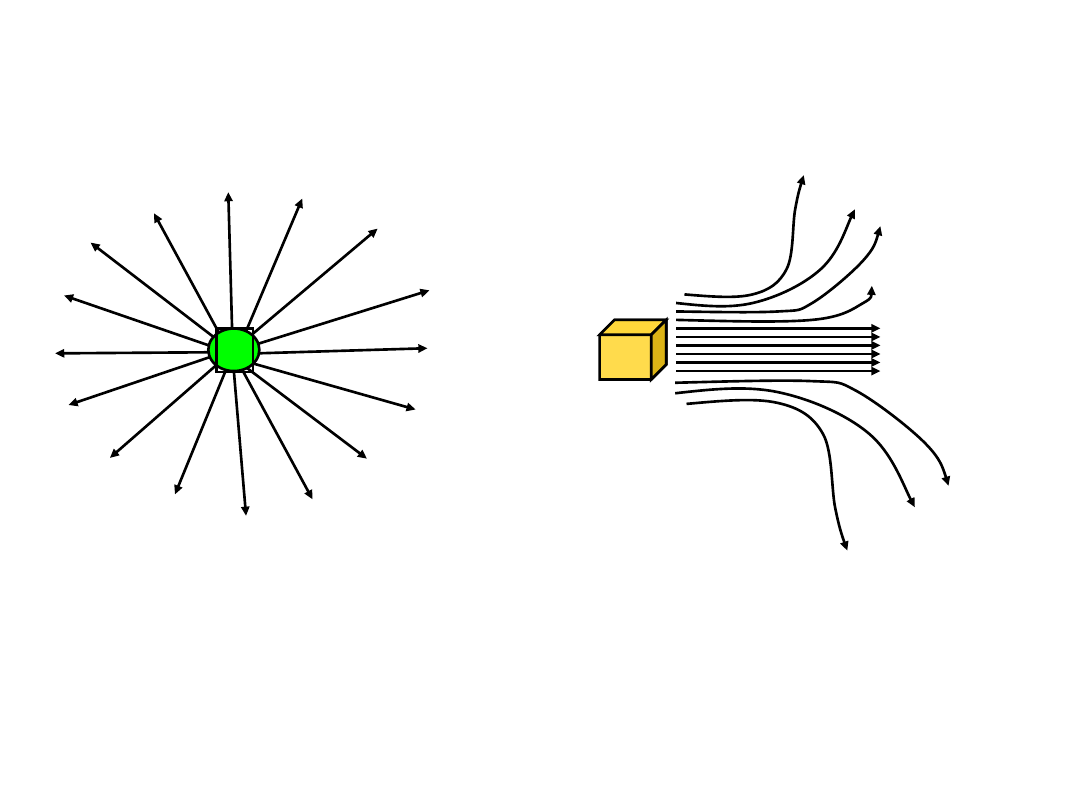
자계의 세기
2
장에서, 전하는,
전기력선을 만들어 방출하며 전계를 형성한다.
마찬가지로,
자기량이 있으면 자기력선을 방출해서 자계를 형성한다.
Q
전기력선이 퍼져 있는 상태를
“전계”라고 함.
E = ·
r 2
Q
0 r
1
전계의세기
m
자기력선이 퍼져 있는 상태를
“자계”라고 함.
H = ·
r 2
m
0 r
1
자계의세기

5.5.3
자계의 세기
H = ·
r 2
m
0 r
1
자계 세기
단위는 [A / m] 혹은 [N / Wb]
예) 자계 세기가 H 인 곳에 자기량 m인 자극을 놓으면 m 이 받는 힘 F는 ; F = mH
예) 전계 세기가 E 인 곳에 전기량 q 를 놓으면 q가 받는 힘 F는 ; F = qE
예) 공기 중에 +2 [Wb]의 자극이 있다. 10 [cm] 떨어진 곳에서의 자계의 세기는
몇 [A / m] 인가 ?
H = ·
r 2
m
0 r
1
에서 공기중이므로
r
H = ·
r 2
m
0
1
= 6.33 × 104
(0.1 m)2
2 [Wb]
= 1.266 × 107 [A / m]

예제) H = 2 [A/m] 의 자계 중에 5 [Wb]의 자극을 놓았을 때 자극이 받는 자력을
구하시오.
H = 2 [A/m]
F =
자극이 있으면, 자기력선을 방출한다. 몇 개의 자기력선을 방출할까 ?
2
장에서, 전하 Q는 매질에서 Q / 진진진진진진진진진진진진진진
진진진진진진진진진진진

5.5.4
자속 및 자속 밀도
자속(磁束; magnetic flux);여러 개의 자력선을 합친 것임.
선 하나는 자력선이라함.
선들을 합친 것은 “속”이라 함.
자속 밀도; 자속이 임의의 면적을 통과할 때, 자력선이 면적당 몇 개가 통과하는가를 말함.

N
자기량이 m [Wb]
인 자극에서 나오는
자력선의 수를 구해보자
자력선 수 N = H × S
2
장에서 ; 전기력선 수 n = E × S
r
H = ·
r 2
m
0
1
진공 혹은 공기중에서 ;
자력선 수 N = H × S =
0
m
0 r
2
m
×
r 2 =
매질에선 자력선 수 N = H × S
m
=

공기에서 자력선 수 N =
0
m
예제) 공기 중에서 1 [Wb]의 자기량이 방출하는 자력선 수를 구하시오 ?
, m =1 [Wb]
이므로 N =
공기에서 자력선 수
0 = 4× 10
-7
[H/m]
이므로
0
1
• 자속밀도 B 의 단위 ; [Wb/m2] 이지만 대신에 [T] 혹은 [G]를 쓴다.
1 Tesla = 105 Gauss = 1 Wb/m2
◈ 자속밀도 B
공기 중에서 자속밀도 B =
0 H
매질 중에서 자속밀도 B =
H
단위 정리
자기량 m 단위 ;
[Wb]
자계 세기 H ; [A/m]
자속 밀도 B ; [Wb/m2]

예제) 공기 중에서 균등자계 H = 3.18× 10 6 일 때 자속밀도 B를 구하시오
예제) 12 [Wb]의 자속과 직각으로 놓인 가로 1.2 m, 세로 0.5 m 인 면에서의 자속밀도는
얼마인가 ?

5.6
자기위치에너지 (자위 磁位)
Note) 2
장에서 전기위치에너지인 전위 V =
전계 세기 × 거리 = E × r 로 정의됨과 유사함.
자기위치에너지 U =
자계세기 × 거리 = H × r
이므로
•
자기위치에너지 단위 U =H × r 에서 H
단위 [ A/m],
거리 r
의 단위 [m]
U
의 단위는 [A]
예제) 공기 중에서 10 [Wb]의 자극으로 부터 2 [m] 떨어진 지점의 자위는 얼마인가 ?

F = ·
r 2
m
1m2
0
1
= 6.33 × 104
r 2
m
1m2
정전계
정자계
전하
Q [C]
자기량
m [Wb]
F = ·
r 2
Q
1Q2
0
1
= 9 × 109
r 2
Q
1Q2
H = ·
r 2
m
0
1
E = ·
r 2
Q
0
1
U = ·
r
m
1
V = ·
r
Q
1
N =
0
m
N =
0
Q
0 = 8,854 × 10
-12
[N ·m2/C2]
0 = 4× 10
-7
[H/m]
≈1.26 × 10 -6 [H/m]
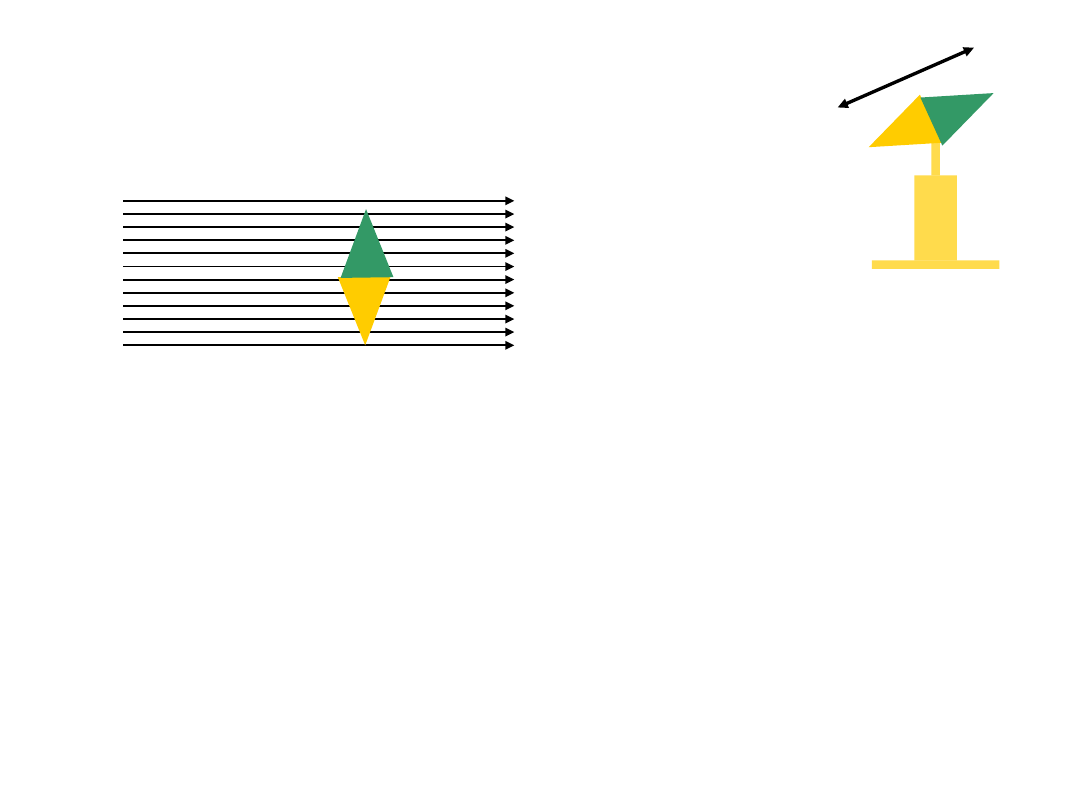
5.3
자기모멘트 (magnet moment)
•
자계는 N극에서 나와 S극으로 간다. 즉, 자계가 나가는 방향에 S극이 있다.
N
S
N
S
l
H
균등자계 H 인 곳에 자기량 m인 자침을 90 o 각도로 놓았다.
•
자계에 놓인 자침은 어느 방향으로 회전을 할까, 회전력은 얼마인가 ?
S
N

균등자계 H 인 곳에 자기량 m인 자침을 90 o 각도로 놓았다.
N
S
H
S
N
① 균등자계 H 에 의해 자기량 m인 자침이 받는 힘 F = mH,
② N 극의 회전력, 즉 토오크
1 = 힘 × 회전중심까지의 수직거리 =
S
극의 회전력, 즉 토오크
1 = 힘 × 회전중심까지의 수직거리 =
③ 전체 토오크
=
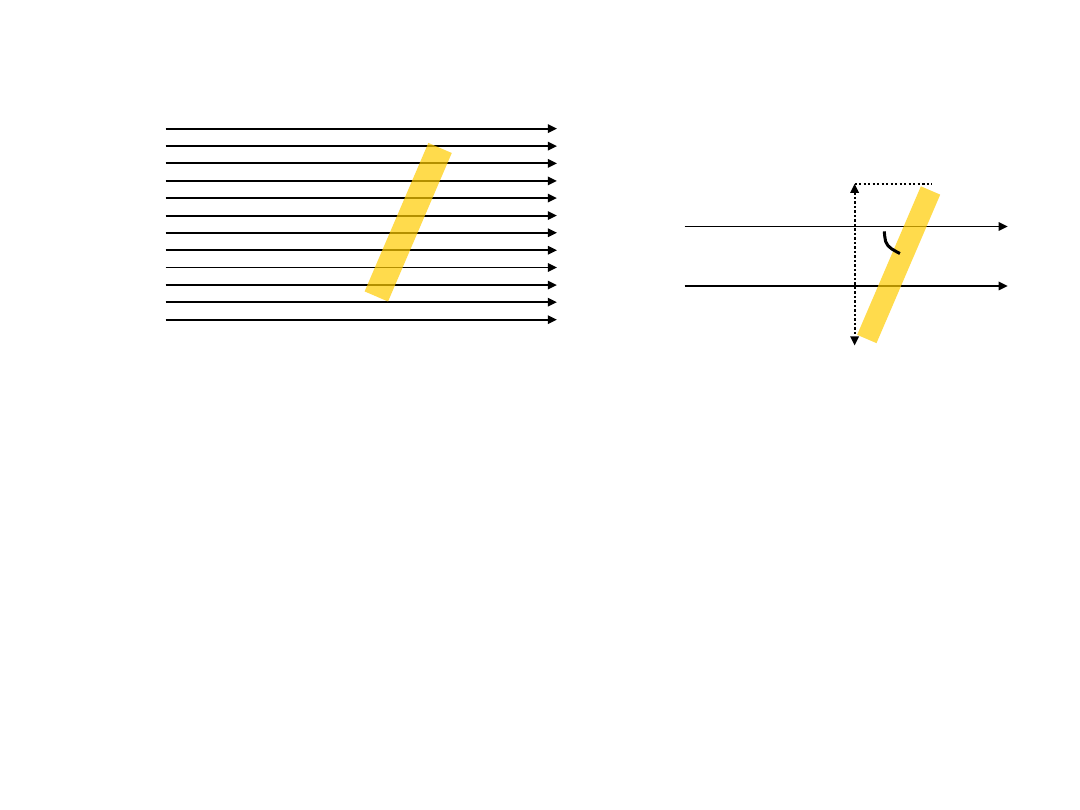
◈ 자침이 균등자계 H 와 각도 를 이룰 때의 토오크
H
S
N
전체 토오크
l sin