
12
장 : 3상회로
12.1
다상 방식의 이점
12.2
기전력의 발생 및 접속
12.3 3
상 회로의 구성
12.4
평형 3상 회로의 전압과 전류
12.5
평형 3상 회로의 등가변환
12.6
평형 3상 회로의 해석
12.7 3
상 회로의 전력
12.8
회전자계
12.9
선로의 전압 강하

◈ 다상방식(多相方式, polyphase system)
☞ 주파수는 같지만 위상이 다른 여러 개의 기전력이 동시에
존재하는 교류 방식
12.1
다상 방식의 이점
► 단상에 비해 송전선을 크게 절약할 수 있다
► 회전자계가 이루어진다.
► 발전,배전,송전 등의 산업용 전력에는 3상방식 사용
► 대칭 3상의 경우, 순시 전력의 총합이 항상 일정하기에
3
상 전동기는 소음과 진동이 작아진다.
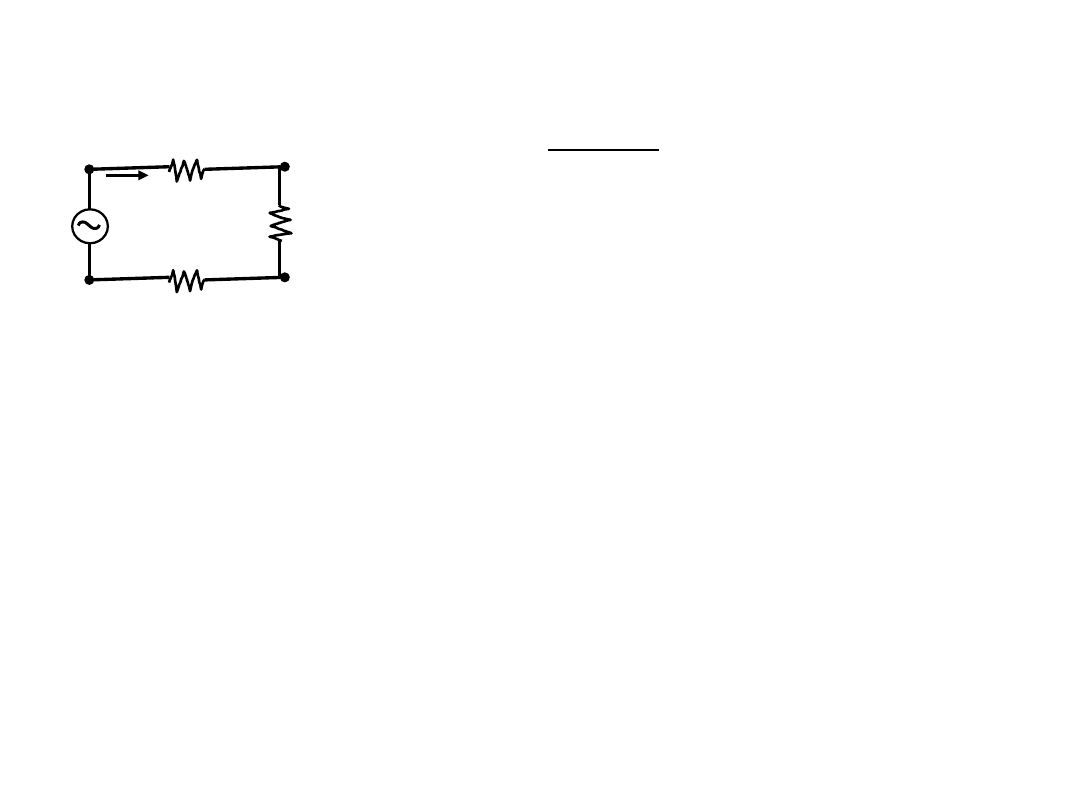
► 선로손실과 다상방식
① 단상송전방식
R
l : 선로저항
전류 I =
R + R
l
V
R(부하)
½ R
l
½ R
l
I
<
단상 송전선로>
V
∴ 부하소비전력 P = I2R [W]
∴ 선로소비전력 P
l = I
2R
l [W]
따라서 부하소비전력 대비 선로소비전력은;
+
-
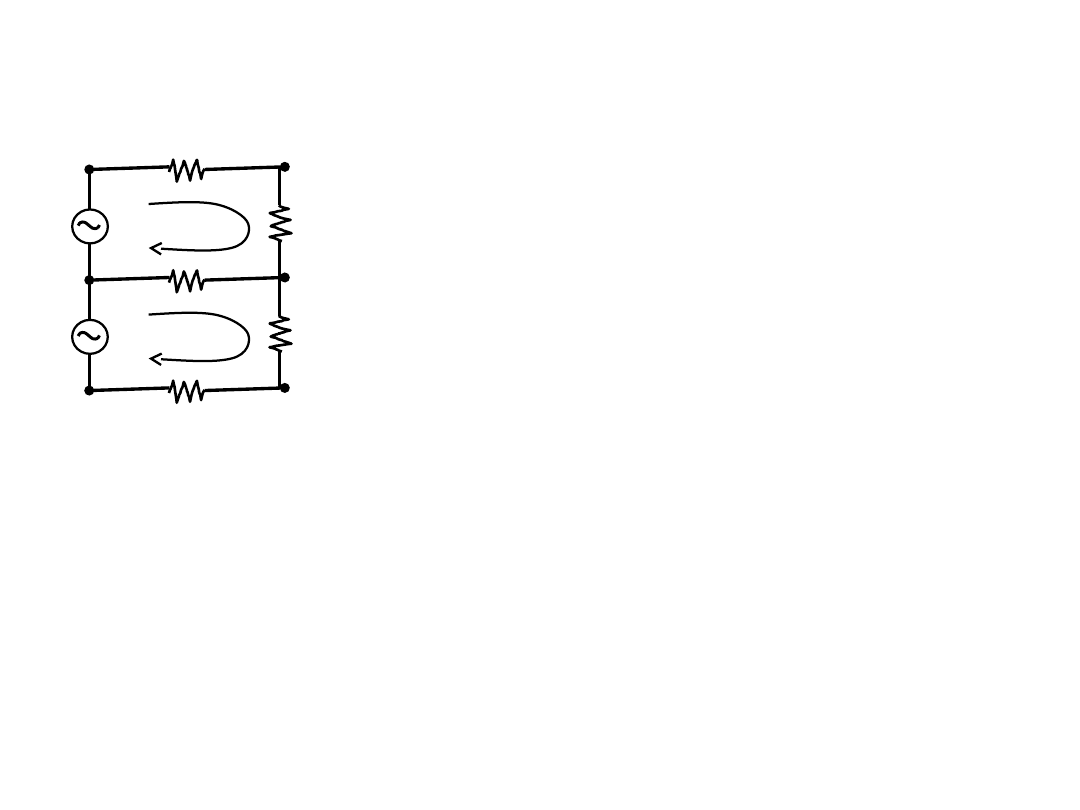
► 선로손실과 다상방식
② 2상송전방식
< 2
상 송전선로>
V
1 = V2 = V 라면,
∴ 선로소비전력 P
l =
따라서 부하소비전력 대비 선로소비전력은;
I
1 = I2 = I0
∴ 부하소비전력 P =
(
중간선로에는 전류가 흐르지 않으므로, 손실 없음)
► 단상방식에 비해 ½로 감소
R(부하)
½ R
l
½ R
l
V
1
R(부하)
½ R
l
V
2
+
-
+
-
I
2
·
I
1
·
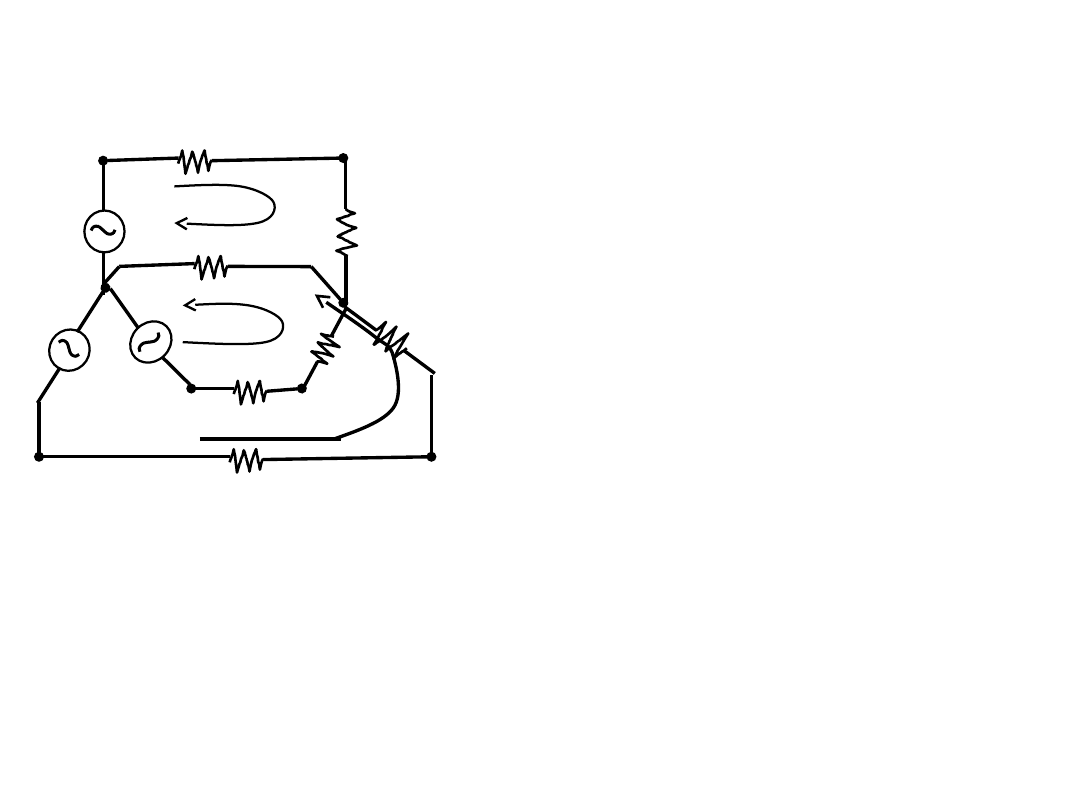
► 선로손실과 다상방식
③ 3상송전방식
V
라면,
∴ 부하소비전력 P = 3I2R [W]
< 3
상 송전선로>
R
½ R
l
+
-
-
+
-
+
½ R
l
R
R
n
n’
I
1
·
I
2
·
I
3
·
V
1
·
V
2
·
V
3
·
V
1
·
= V
2
·
= V
3
·
=
I
I
1
·
= I
2
·
= I
3
·
=
► 전압의 크기가 같고 위상이 1200 차이가 나면,
순시값의 합이나 벡타 합은 항상 “0”임.
따라서 전류도 순시값의 합이나
벡타 합은 항상 “0”임. 즉,
►또한 중성선 n – n’ 에 흐르는 전류는 “0” 이다 ∴ 선로소비전력 P
l = 1.5 I
2R
l [W]
따라서 부하소비전력 대비 선로소비전력은;
► 단상방식에 비해 ½로 감소
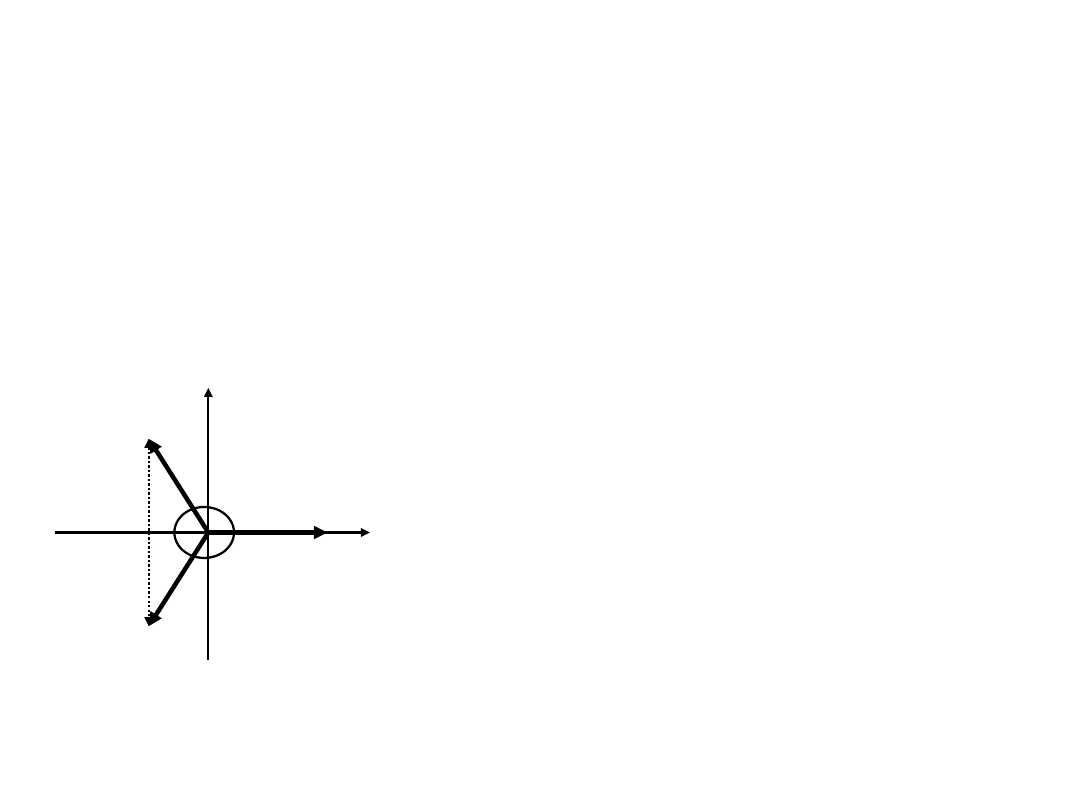
◈ 전압의 크기가 같고 위상이 1200 차이가 나면,
순시값의 합이나 벡타 합은 항상 “0”임.
► 순시전압
v
1 + v2 + v3 = Vm [sint + sin(t - 120
0
) + sin(t + 1200)]
sin(t - 1200) = sint cos 1200 - cost sin 1200
sin(t + 1200) = sint cos 1200 + cost sin 1200
► sint + sin(t - 1200) + sin(t + 1200)= sint + 2sint cos 1200 = 0
∴ 순시값의 합
V
1x
·
= V
1
V
1y
· = 0
V
2y
·
V
3y
·
+
= 0
1200
1200
V
1
·
V
2
·
V
3
·
600
V
2y
V
3y
V
2x =
V
3x =
∴ V
1x + V2x + V3x =
(∵ V
1 = V2 = V3 )
∴ 벡타의 총합 V
1
·
= 0
V
2
·
+
V
3
·
+
12.2
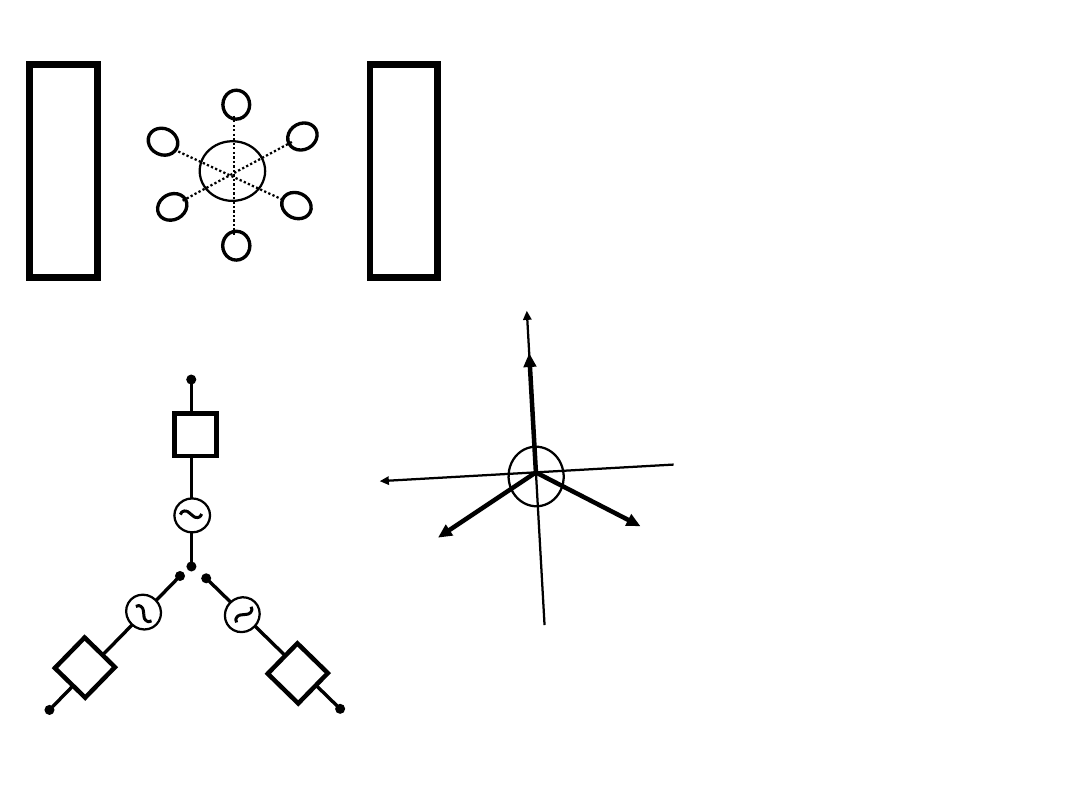
기전력의 발생 및 접속
N
S
●
X
●
X
●
X
a
x
b
y
c
z
►동일 구조의 3개의 권선을 1200 간격으로
전기자에 감는다.
►전기자가 일정한 속도로 회전하면, 각 권선
양단에 크기는 같고 위상이 1200 차이가 나는 3
개의 단상교류전압이 유도
►3
개의 단상전압을 총칭해서 3상 전압이라 함.
V
a
·
+
-
Z
g
·
a
x
V
c
·
+
-
Z
g ·
c
z
V
b
·
+
-
Z
g
·
b
y
< 3
상전원의 등가표시>
< 3
상발전의 기본 원리>
12
0
0
12
0
0
12
0
0
V
a
·
V
c
·
V
b
·
V
1
·
= 0
V
2
·
+
V
3
·
+
∴ 전압의 총합은 항상 “0” 임
►
따라서 전원 내부에 순환 전류는
흐르지 않는다.
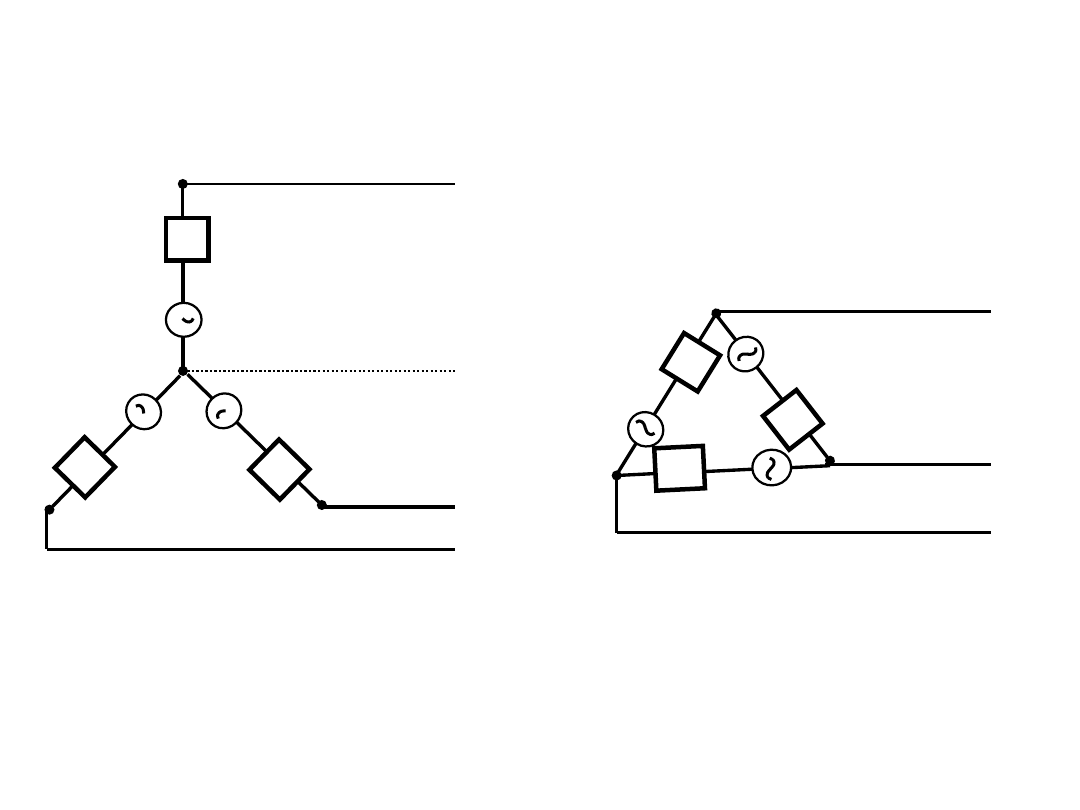
☞ 평형 3상전원( 혹은 대칭 3상전원)
3
상 전원의 위상은 1200 차이가 나지만, 전원의 크기와 내부 임피던스가
같은 전원을 말함.
Z
g
·
V
a
·
+
-
a
V
c
·
+
-
Z
g ·
c
V
b
·
+
-
Z
g
·
b
중성선
<Y
결선>
<
결선>
Z
g
·
V
a
·
+
-
V
b
· +
-
Z
g
·
V c
·
+
-
Z
g
·
b

12.3 3
상 회로의 구성
►3
상 전원에 부하를 접속하여 구성하는 3상 회로는
부하측도 Y 혹은 결선이 될 수 있다.
< 3
상전원의 등가표시>
►따라서 전원부와의 조합방식에 따라, 등의
방식으로 구분된다.
►전원과 부하측이 모두 대칭일 때, “평형 3상 회로 혹은 평형 3상교류” 라 하며,
그렇치 않은 경우를 “불평형 3상 회로 혹은 불평형 3상교류” 라 함.
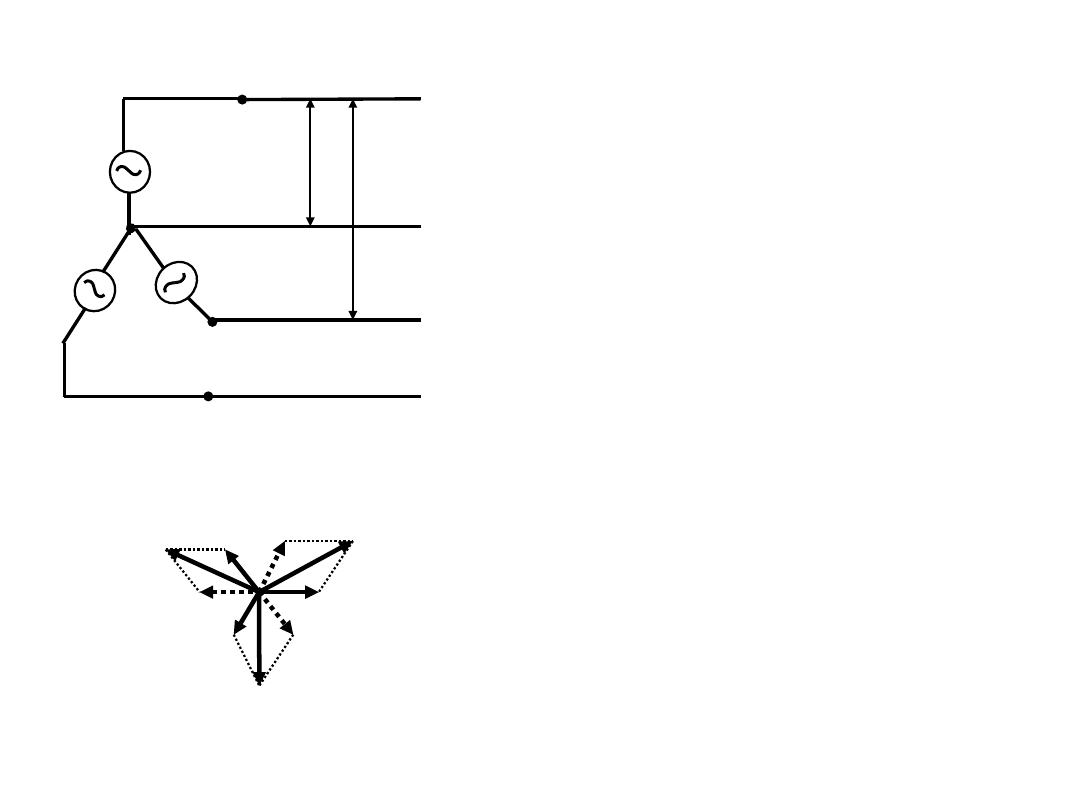
12.4
평형 3상 회로의 전압과 전류
I
la
·
+
-
-
+
-
+
n
V
a
·
V
b
·
V
c
·
V
ln
·
V
lab
·
I
c
·
I
b
·
I
a
·
I
lb
·
I
lc
·
<
이상적인 평형 3상 Y 결선 회로>
각 단상의 상전압을
V
a
·
V
b
·
,
V
c
·
,
단상 전원의 상전류를 Ia
·
I
b
·
,
I
c
·
,
I
a
·
= I
la
·
I
b
·
= I
lb
·
I
c
·
= I
lc
·
► 상전류와 선전류는 같다, 즉
►
선간전압은 각 전원의 전위차이므로, 즉,
V
lab
·
= V
a
·
- V
b
·
V
lbc
·
= V
b
·
- V
c
·
V
lca
·
= V
c
·
- V
a
·
V
lab
·
V
lbc
·
V
lca
·
V
a
·
-V
a
·
V
b
·
-V
b
·
-V
c
·
V
c
·

☞ 해석
V
lab
·
V
a
·
- V
b
·
V
a
·
+ ( - )
V
b
·
는
로
, 이는 와 같다.
또한
,
사잇각은 600 이므로,
V
a
·
와 ( - )
V
b
·
V
lab
·
V
a
·
와
의 사잇각은 300 , 또한
V
lab
·
-V
b
·
와
의 사잇각도 300 이다.
V
lbc
·
V
lca
·
와
도 동일허게 성립한다.
►
평형3
상회로에서 선간전압은
√
단상전압의 3
배가 된다.
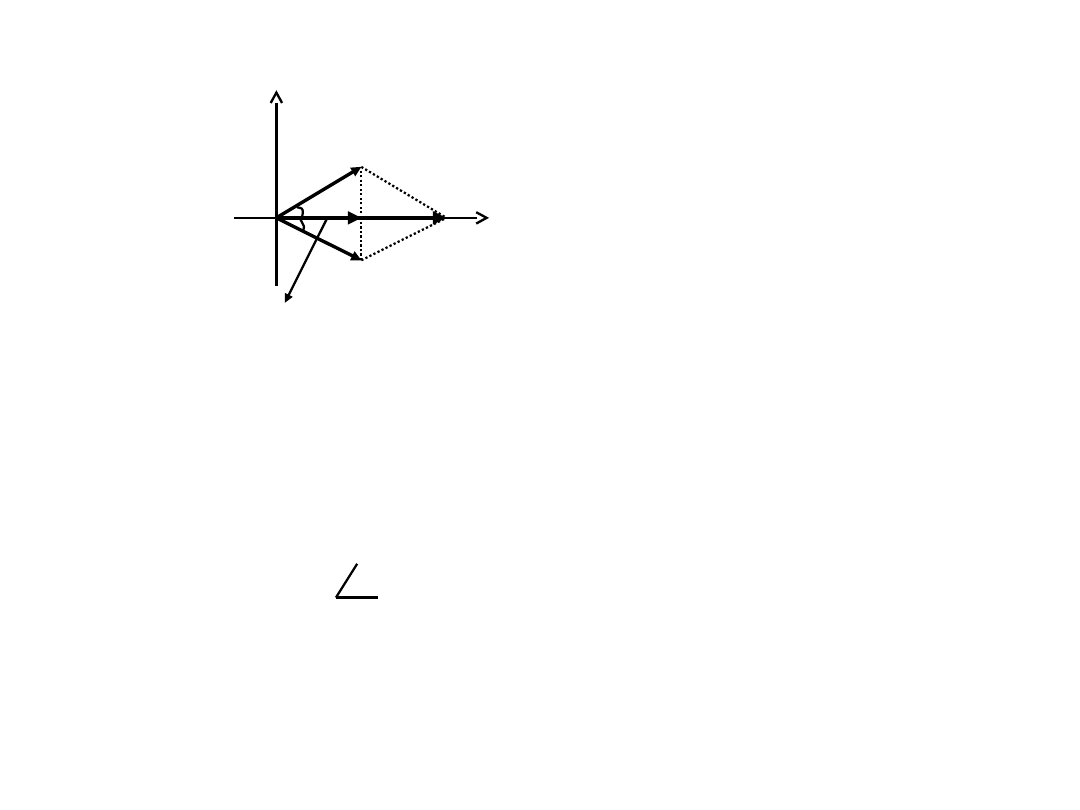
V
a
-V
b
V
a +(- Vb)
► V
a +(- Vb)의 y 축 성분은 “0” 이 되고,
► V
a +(- Vb)의 x 축 성분은 Va cos 30
0
의 2배 즉, √3 V
a
(∵ V
a 와 (- Vb)의 위상차는 60
0
이지만, 크기는 같음)
►
√
선간전압은 단상전압의 3 배
V
a cos 30
0
+ (- V
b cos 30
0
) = √3V
a / 2 + √3(-Vb) / 2 = √3Va
300
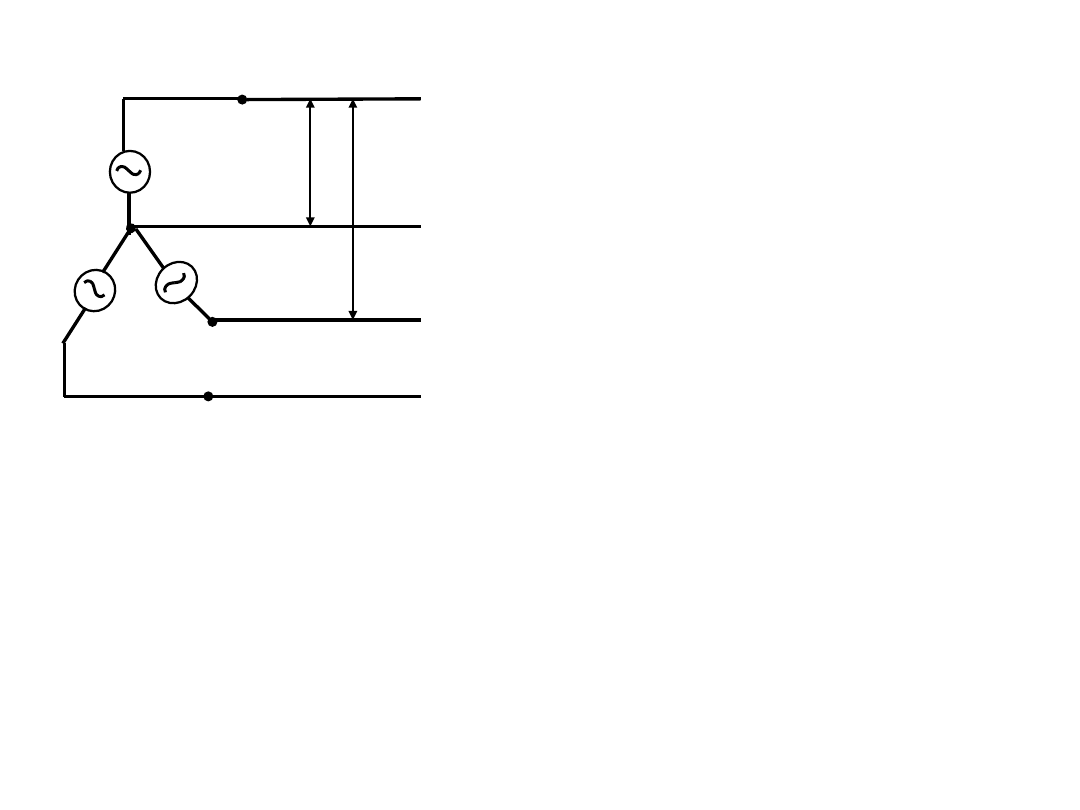
► 평형 3상 4선삭 회로의 상전압과 선간전압
I
la
·
중성선의 전위는 “0”이므로,
V
b
·
V
nb
·
=
V
a
·
V
na
·
=
V
c
·
V
nc
·
=
∴ V
lab
·
=
∴ V
lbc
·
=
∴ V
lca
·
=
► 평형 3상 4선삭 Y 결선 회로의 전압,전류 관계식
상전류 I
p
·
단상 전원의 상전류를 Ia
·
I
b
·
,
I
c
·
,
선전류 I
l
·
상전압 V
p
·
선간전압 V
l
· 선로와 중성선 사이의 전위차 Vln
·
+
-
-
+
-
+
n
V
a
·
V
b
·
V
c
·
V
na
·
V
lab
·
I
c
·
I
b
·
I
a
·
I
lb
·
I
lc
·
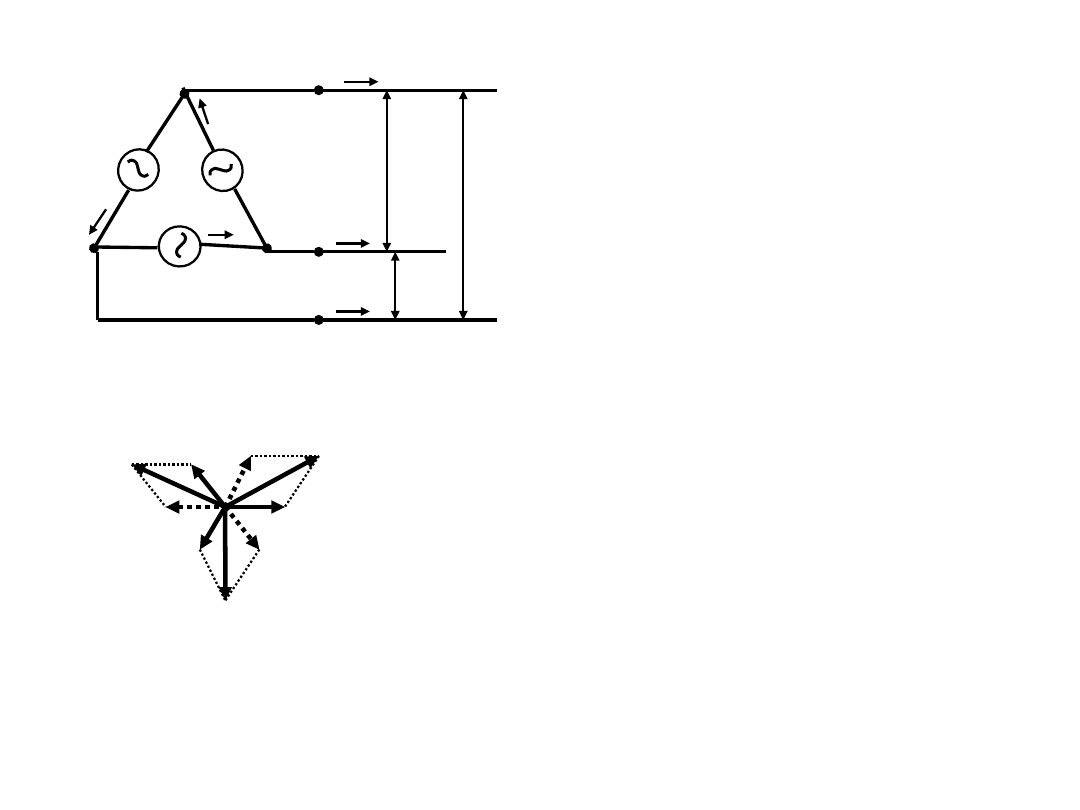
☞ 평형 3상 결선 회로에서,
► 상전압과 선간전압은 크기와 위상이 일치
∴ V
lab
·
= V
a
·
V
lbc
·
= V
b
·
V
lca
·
= V
c
·
V
lab
·
I
c
·
I
b
·
+
-
Va
·
V
b
·
+
-
-
+
V
c
·
I
a
·
I
lc
·
I
lb
·
V
lbc
·
V
lca
·
b
a
c
I
la
·
I
b
· I
lb
·
I
a
·
=
+
I
b
·
I
lb
·
I
a
·
=
+ (- )
►
I
c
· I
lc
·
I
b
·
=
+
I
c
·
I
lc
·
I
b
·
=
+ (- )
►
I
la
·
I
lb
·
I
lc
·
I
a
·
- I
a
·
I
b
·
- I
b
·
- I
c
·
I
c
·
► 선간 전류는 상전류의 √3 배임
► 평형 3상 결선 회로의 전압,전류 관계식
상전류 I
p
·
선전류 I
l
·
상전압 V
p
·
선간전압 V
l
·

예제12-1) 형 평형 3상 회로의 선로에 30 [A]의 전류가 흐르고 있다.
부하 한 상의 임피던스가 (3+j4) [] 일때, 부하의 상전류, 상전압,
및 선간 전압의 크기를 구하시오.
의 관계식으로 부터,
= 3+j4 []
Z
·
상전압
선간전압
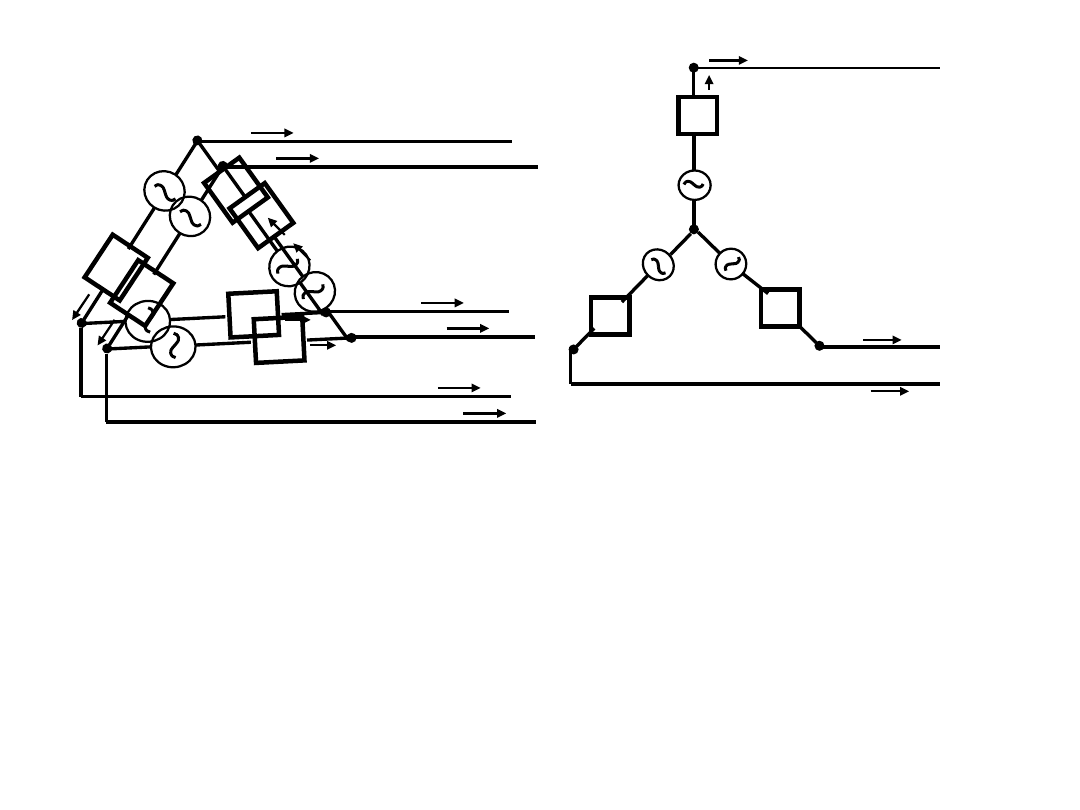
12.5
평형 3상 회로의 등가변환
+
-
Z
·
V
12
·
Z
·
+
-
V
23
·
+
-
Z
·
V
31
·
3
2
1
I
12
·
I
1
·
I
2
·
I
3
·
I
23
·
I
31
·
Z
Y
·
V
1
· +
-
1
+
-
3
+
-
2
<Y
결선>
I
1
·
I
2
·
I
3
·
Z
Y
·
Z
Y
·
V
2
·
V
3
·
► 평형 3상 결선과 Y결선은 상호 하다.
► 이를 위해서는 각 선간전압(혹은 단자전압)이 같으면 된다.
각 단자전압을, V
12’
·
, V
23
’
·
V
31
’
·
,
라 하면,
► 평형 3상 결선에서,
+
-
Z
·
V
12
·
Z
·
+
-
V
23
·
+
-
Z
·
V
31
·
3
2
1
I
12
·
I
1
·
I
2
·
I
3
·
I
23
·
I
31
·
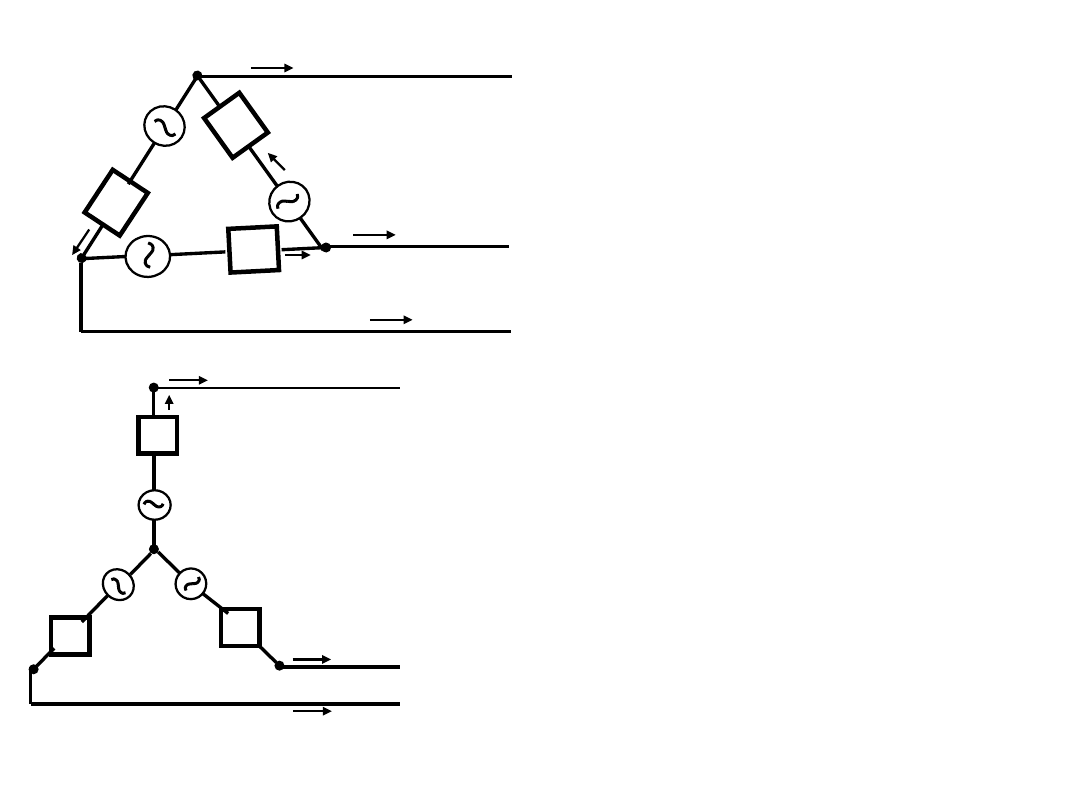
각 단자전압, V12’
·
, V
23
’
·
V
31
’
·
,
V
12
’
·
= V12
·
Z
I
12
· ·
-
V
12
’
·
= V1
·
Z
YI1
· ·
-
- V
2
·
Z
YI2
· ·
-
( ) ( )
► 평형 3상 결선에서,
► 평형 3상 Y결선에서,
► 와 Y결선에서, V
12’, V23’, V31’ 을 같다고 두면,
V
12
·
Z
I
12
· ·
-
= V1
·
Z
YI1
· ·
-
- V
2
·
Z
YI2
· ·
-
( ) ( )
따라서 V
12
·
Z
I
12
· ·
=
=
I
1
·
+
-
Z
·
V
12
·
Z
·
+
-
V
23
·
+
-
Z
·
V
31
·
3
2
1
I
12
·
I
2
·
I
3
·
I
23
·
I
31
·
Z
Y
·
V
1
· +
-
1
+
-
3
+
-
2
<Y
결선>
I
1
·
I
2
·
I
3
·
Z
Y
·
Z
Y
·
V
2
·
V
3
·
따라서 V
12
·
= V1
· - V
2
·
Z
I
12
· ·
= Z
YI1
· ·
Z
YI2
· ·
-
동일한 방법으로, V
23
’
·
V
31
’
·
,
에 관해 구할 수 있으며, 정리하면,
=
I
1
· -
Z
Y
·
I
2
·
( )
V
12
·
= V1
· - V
2
·
Z
I
12
· · =
I
1
· -
Z
Y
·
I
2
·
( )
V
23
·
= V2
· - V
3
·
Z
I
23
· · =
-
Z
Y
·
I
3
·
( )
I
2
·
V
31
·
= V
3
· - V
1
·
Z
I
31
· · =
-
Z
Y
·
I
1
·
( )
I
3
·
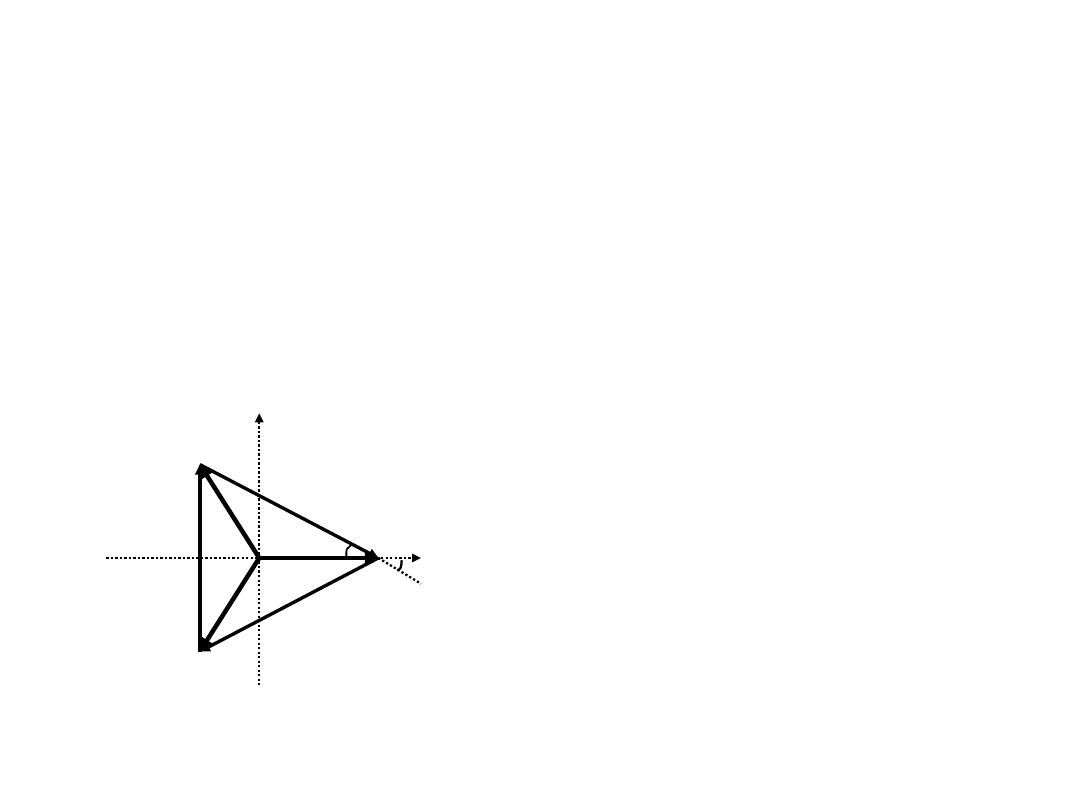
의 위상도로
V
1
· V
2
· V
3
·
V
12
·
, V
23
·
V
31
·
,
관계식을 구한다
.
☞
V
1
·
V
2
·
V
3
·
V
12
·
V
23
·
V
31
·
►V
1, V2 , V3 의 크기는 같다.
►
V
1V2V12 에서, V12 는 V1보다 √3베 크며,
►
V
1V2V12 에서, V1 과 V2보의 사잇각은 120
0
► 따라서 V
1과 V12 ( 또한V2 와
V12 )의 사잇각은 30
0
즉, V
12 는 V1 보다 앞선다.
►
V
2V3V23 와 V1V3V31 서에서도 유사한
결과를 구할 수 있다.

☞ 결론적으로
,
► 결선의 상전압
는 Y 결선의 상전압 V
1
· V
2
· V
3
·
V
12
·
, V
23
·
V
31
·
,
보다
크기는 √3베 크고 위상이 300 앞선다, 즉,
V
12
·
= V
1
· - V
2
· =
V
31
·
= V3
· - V
1
· =
① Y 전원에서 전원으로 변환할 때,
② 전원에서 Y 전원으로 변환할 때,
V
1
·
=
V
2
·
=
V
3
·
=
√3
V
31
·
-300
1
☞ 임피던스 관계식
Z
I
12
· · =
I
1
· -
Z
Y
·
I
2
·
( ) Z
I
23
· · =
-
Z
Y
·
I
3
·
( )
I
2
·
Z
I
31
· · =
-
Z
Y
·
I
1
·
( )
I
3
·
I
1
·
= 0
I
2
·
+
I
3
·
+
관계식 이용
=
I
12 – I31
· ·
I
1
·
관계식으로 부터
+
-
Z
·
Z
·
+
-
+
-
Z
·
3
2
1
30
0
0
[V]
30
120
0
[V]
30
-120
0
[V]
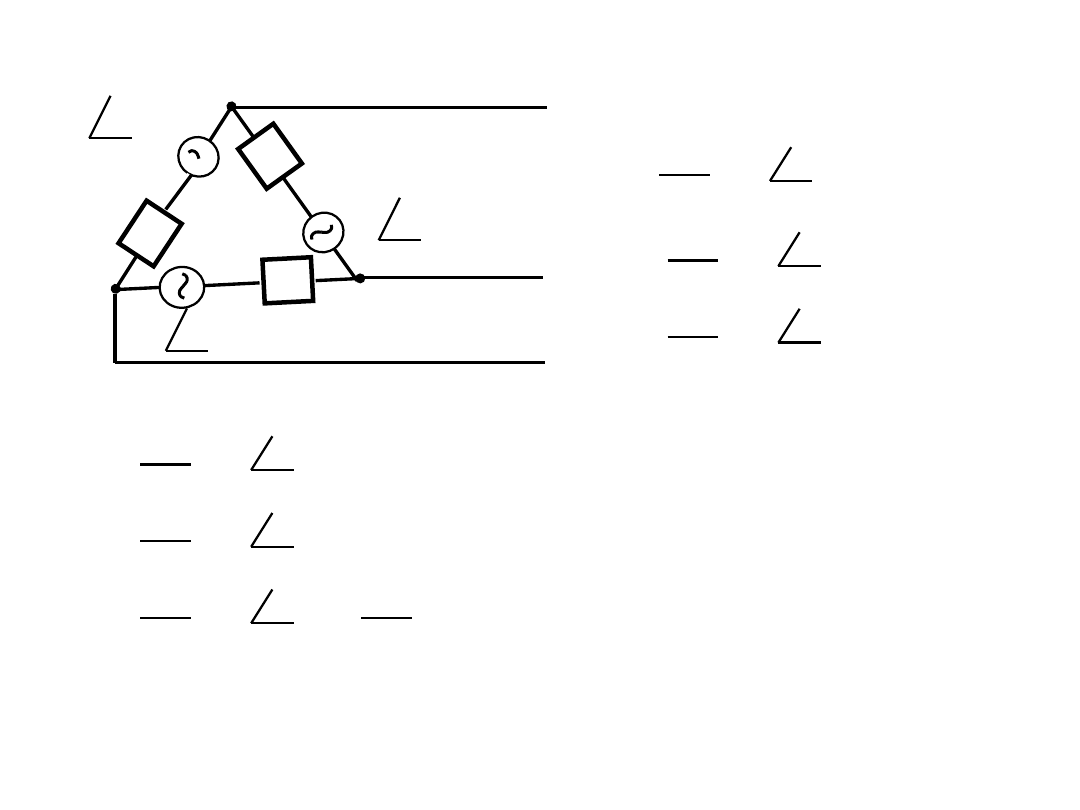
= 0.3+j0.6 []
Z
·
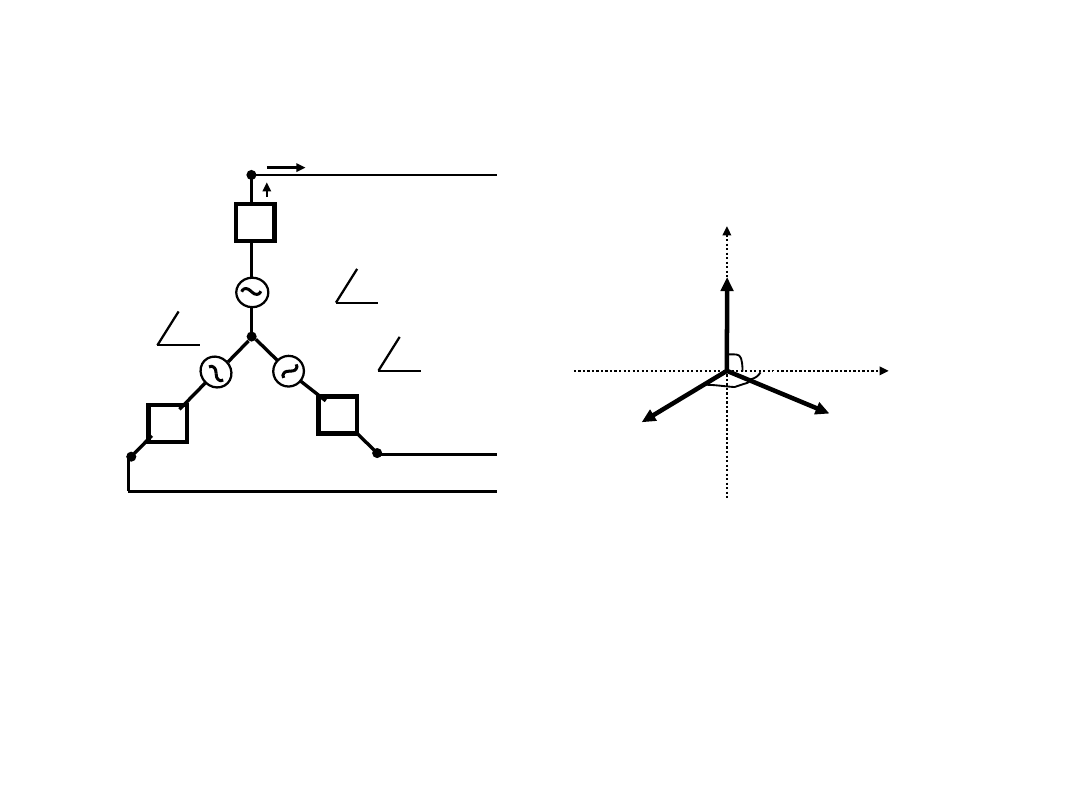
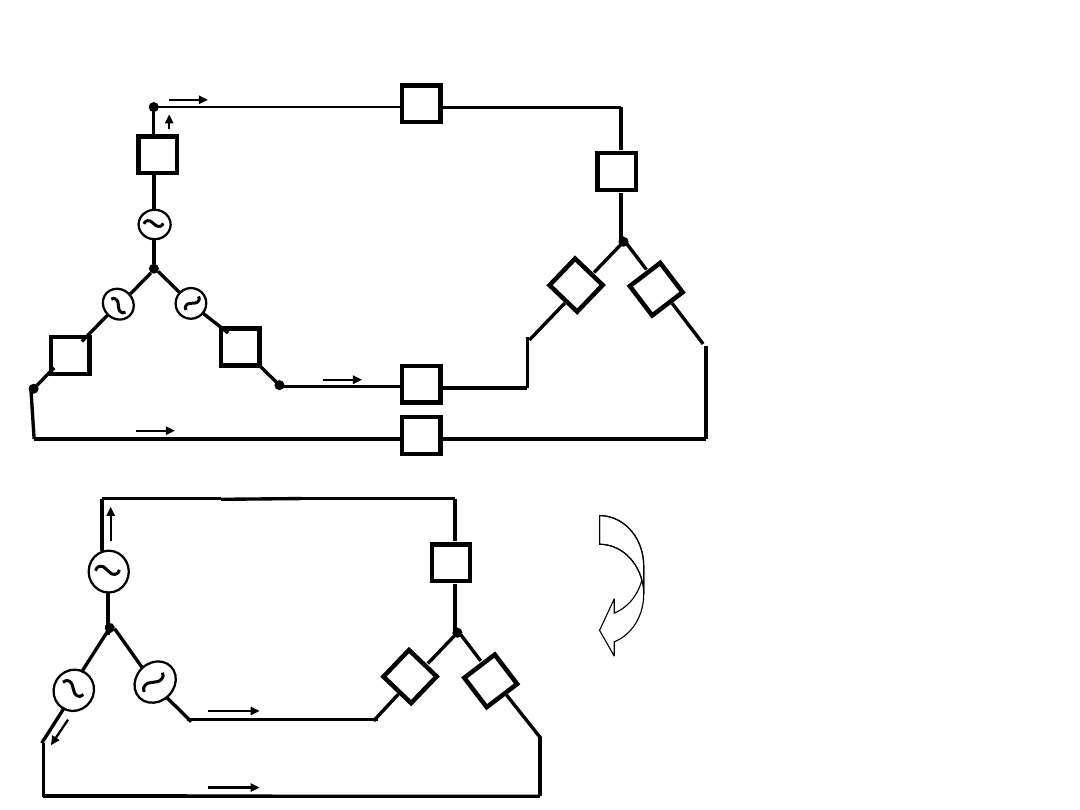
예제 12.2 아래의 형의 평형 3상회로를 Y형으로 등가변환하시오.
② 전원에서 Y 전원으로 변환할 때,
V
1
·
=
√3
V
12
·
-300
1
V
2
·
=
√3
V
23
·
-300
1
V
3
·
=
√3
V
31
·
-300
1
V
1
·
=
√3
V
12
·
-300
1
V
2
·
=
√3
V
23
·
-300
1
V
3
·
=
√3
V
31
·
-300
1
=
√3
-300
30
1200
= 17.3 90
0
= 3 Z
Y
·
Z
·
= 0.1+j0.2 []
Z
Y
·
Z
Y
·
Z
Y
·
+
-
1
+
-
3
+
-
2
<Y
결선>
I
1
·
Z
Y
·
Z
Y
·
17.3 -300
17.3 -1500
17.3 900
V
1
·
V
2
·
V
3
·
300
1500
900
12.6
평형 3상 회로의 해석
Z
g
·
+
-
+
-
+
-
I
a
·
Z
g
·
Z
g
·
Z
l
·
Z
l
·
Z
l
·
I
b
·
I
c
·
Z
L
·
Z
L
·
ZL
·
+
-
-
+
-
+
n
V
a
·
I
c
·
I
a
·
I
b
·
I
c
·
Z
0
·
Z
0
·
Z0
·
Z
0
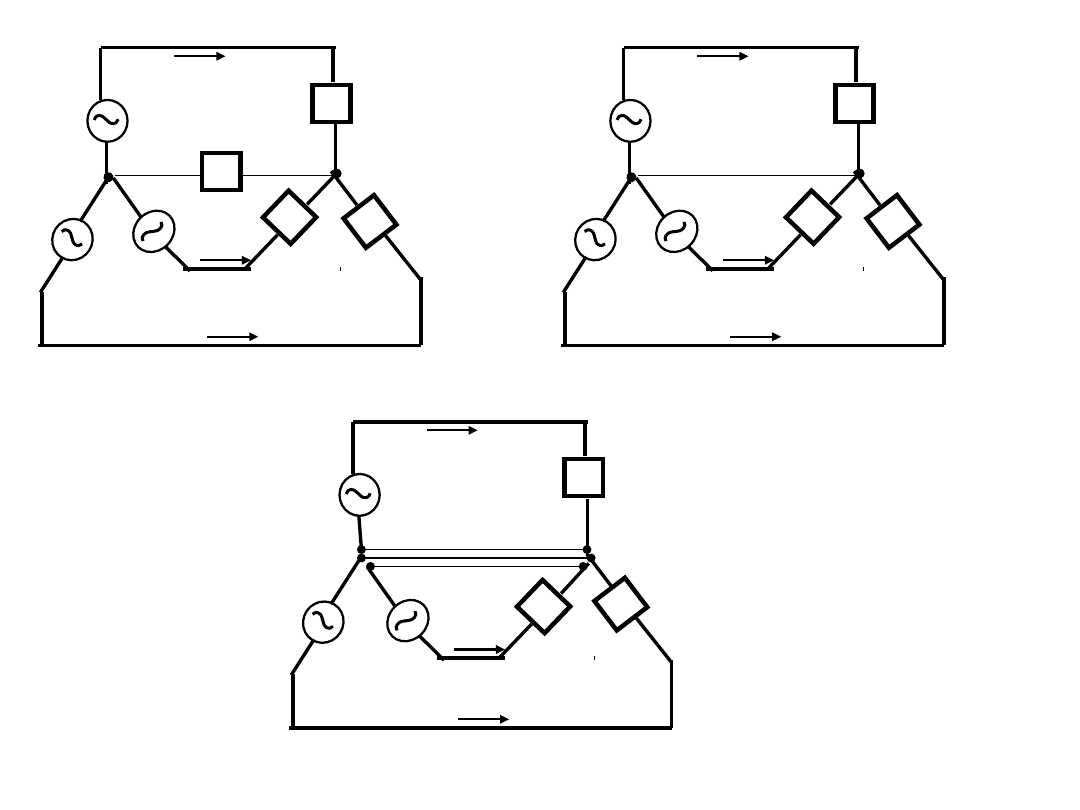
· = + +
Z
g
· Z
l
· Z
L
·
를 하나의 임피던스로 두면,
Y-Y
평형 3상회로는
간략해진다.
+
-
-
+
-
+
n
V
a
·
I
b
·
I
c
·
Z
0
·
Z
0
·
Z0
·
n’
I
a
·
V
c
·
V
b
·
Z
n
·
+
-
n
V
a
·
Z
0
·
n’
I
a
·
-
+
I
b
·
Z
0
·
V
b
·
-
+
I
c
·
Z0
·
V
c
·
(c)
+
-
-
+
-
+
n
V
a
·
I
b
·
I
c
·
Z
0
·
Z
0
·
Z0
·
n’
I
a
·
V
c
·
V
b
·
(d)
(e)
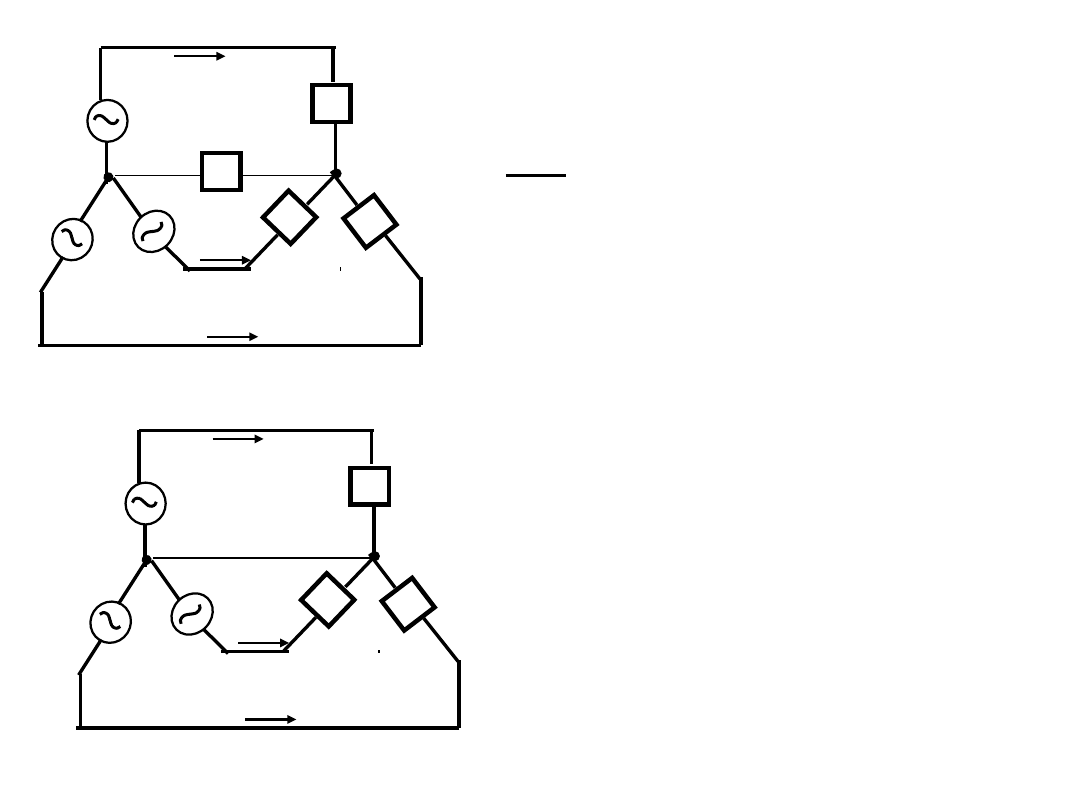
(c), (d), (e)
회로가 등가임을
증명하자
(c)
► 밀만의 정리를 통해 중성선에 전위가 “0” 임을 증명
V
a
·
= 0
V
b
·
+
V
c
·
+
Y=
단위 [υ] ; “mho”
·
Z
·
[υ]
∴ 중성선 전위는 “0” 임
Note that
► 평형 3상 Y 결선 회로에서 중성선 에는
전류가 흐르지 않으므로, 이 가능하다.
∴ (c)와 (d)는 등가
+
-
-
+
-
+
n
V
a
·
I
b
·
I
c
·
Z
0
·
Z
0
·
Z0
·
n’
I
a
·
V
c
·
V
b
·
Z
n
·
+
-
-
+
-
+
n
V
a
·
I
b
·
I
c
·
Z
0
·
Z
0
·
Z0
·
n’
I
a
·
V
c
·
V
b
·
(d)
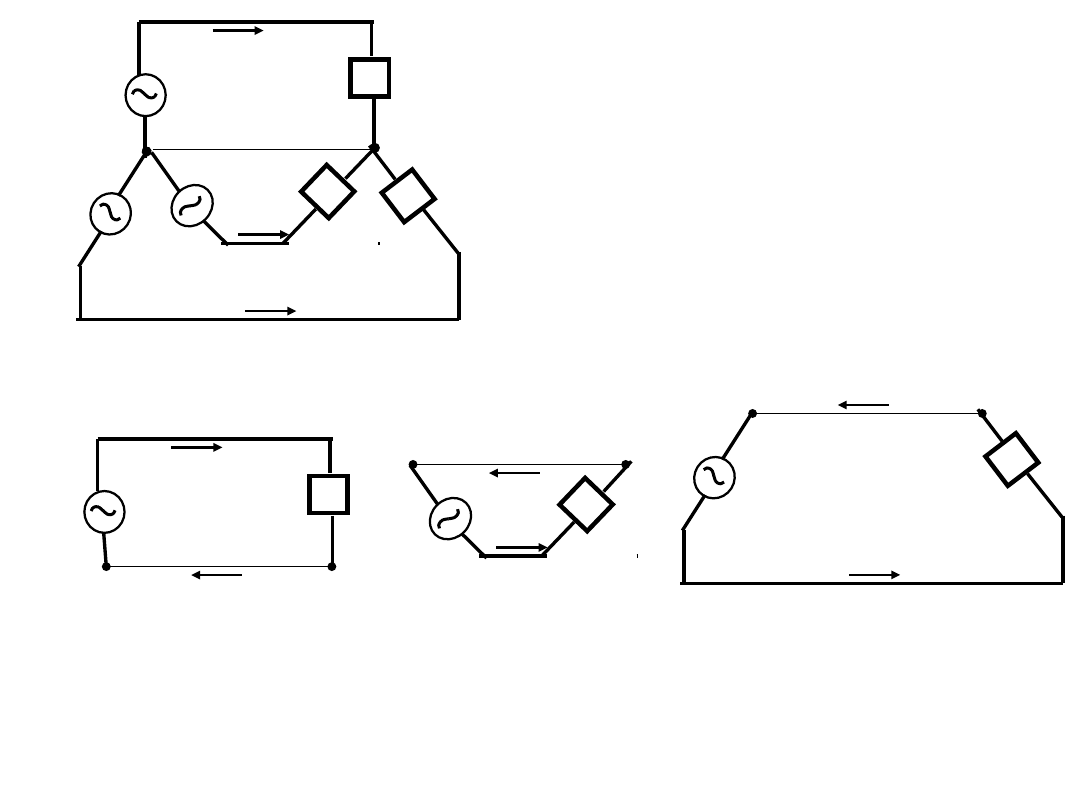
► 중성선은 단락, 따라서
I
a
·
는 모두 중성선
으로 흐른다;
I
b
·
,
I
c
·
,
즉 , 이들 전류가 흐르는 회로만을 분리하면,
(d-1),(d-2),(d-3)
회로가 된다
+
-
n
V
a
·
Z
0
·
n’
I
a
·
I
a
·
(d-1)
-
+
I
b
·
Z
0
·
V
b
·
n
n’
I
b
·
(d-2)
-
+
I
c
·
Z0
·
V
c
·
n
n’
I
c
·
(d-3)
따라서, (d-1),(d-2),(d-3) 은 평형 3상회로의
등가단상 회로가 된다.
+
-
-
+
-
+
n
V
a
·
I
b
·
I
c
·
Z
0
·
Z
0
·
Z0
·
n’
I
a
·
V
c
·
V
b
·
(d)

☞ 결론적으로, (c),(d),(e) 는 등가이다. 그러므로, Y-Y 결선의 3선4선식
평형 3상 회로는 3개의 단상회로로 변환할 수 있다.
☞ 따라서, 회로의 전력은 각 단상 회로의 전력을 합한 값과 같다.
☞ 따라서, 회로의 전력은 각 단상 회로의 전력을 합한 값과 같다.
☞ 본 장은, Y-Y 결선에 대해 고려했지만, 대칭 3상 회의 전원이나 부하는
Y
변환이 가능하기 때문에 어떠한 평형 3 상 회로는 Y-Y 결선으로
변환이 가능하다.
V
ab
·
I
c
·
I
b
·
+
-
+
-
-
+
I
a
·
V
bc
·
V
ca
·
Z
l
·
Z
l
·
Z
l
·
Z
L
·
Z
L
·
ZL
·
+
-
V
a
·
Z
0
·
I
a
·
I
a
·
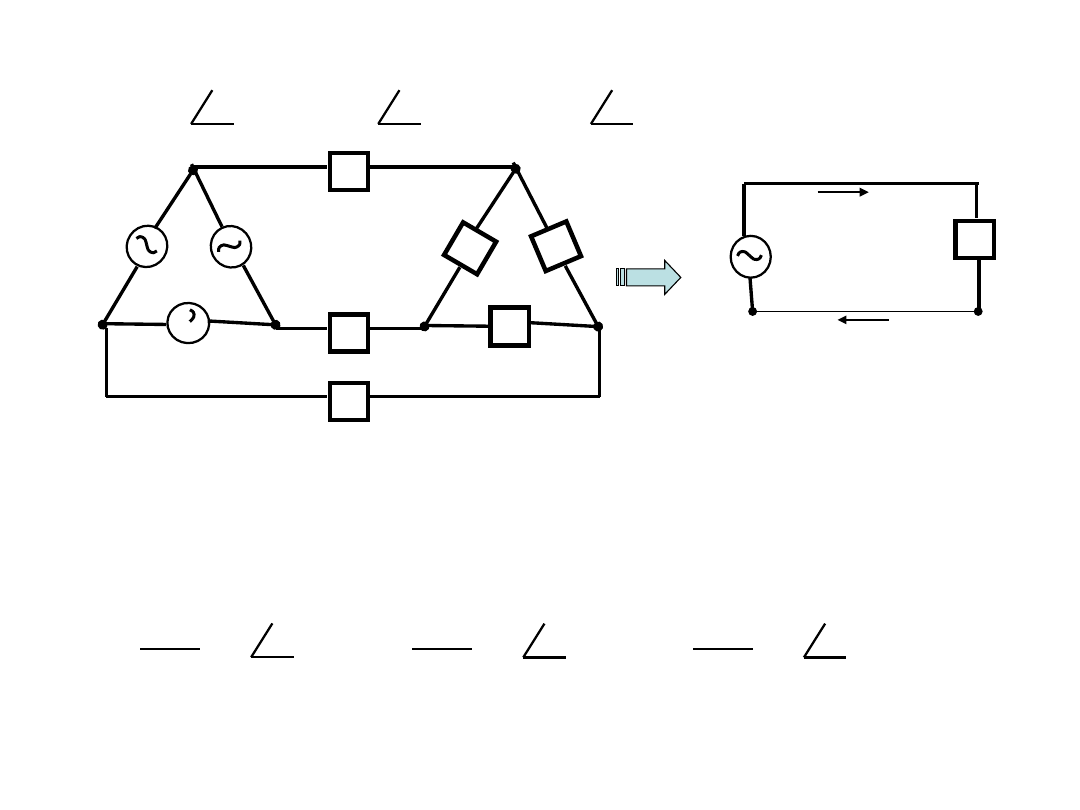
예제 12.3) 아래와 같은 평형 3상 회로에서 선전류 및 전원에서
공급되는 유효전력의 총합을 구하시오. 단,
V
ab
·
180 00
=
V
bc
·
180 -1200
=
V
ca
·
180 1200
=
Z
l
· = 11 [
]
Z
L
· = 21 +j72[
]
= 3 Z
Y
·
Z
·
► Y
변환에서 임피던스 관계는,
►
따라서,
=
Z
·
► 12.5
절,
② 전원에서 Y 전원으로 변환할 때,
V
1
·
=
√3
V
12
·
-300
1
V
2
·
=
√3
V
23
·
-300
1
V
3
·
=
√3
V
31
·
-300
1
►
따라서,

►
= 18 + j24 [] = 6(3+j4) []
Z
·
►
따라서,
V
a
· = 60√3 -300
V
a
·
Z
0
·
10√3
-300
I
a
· = =
3+j4
=
►
따라서, P
a =
∴
전체 부하 전력은 P =3P
a =

12.7 3
상 회로의 전력
► 결선 방식이나 평형 혹은 불평형에 관계없이 각 상에서의
전력을 구한 후 합산한다.
► 부하에서의 상전압과 상전류를 각각
그리고 각상전압과 전류의 위 상차를
abc 라라
V
a
· V
b
· V
c
· I
a
· I
b
· I
c
·
► 평형회로에서 각 상전압과 상전류의 크기는 같아야 한다 즉,
► V
a = Vb = Vc = Vp , Ia = Ib = Ic = Ip , a = b = c =
∴P = 3 V
pIp cos
●
선간전압
V
l 선전류 Il 에 의한 표기
► 복소전력 P
a
· = P + jP
r =

12.7 3
상 회로의 전력
●
선간전압
V
l 선전류 Il 에 의한 표기
=
V
l
·
V
p
·
= √3
I
l
·
I
p
·
300
① 결선
의 관계식에서
크기는; V
l = Vp , Il = √3 Ip
∴P = 3 V
pIp cos Pr= 3 VpIp sin
=
I
l
·
I
p
·
= √3
V
l
·
V
p
·
300
② Y 결선
의 관계식에서
크기는; V
l = √3Vp , Il = Ip
∴P = 3 V
pIp cos Pr= 3 VpIp sin
∴ 결선과 Y 결선에서; P = 3 V
pIp cos √3 Vl Ilcos
P
r= 3 VpIp sin √3 Vl Ilsin

●
선간전압
V
l 선전류 Il 에 의한 피상전력 표기
P
a
· = P + jP
r = 3 VpIp ( cos + j sin
의 관계식에서
►
P
a = 3 VpIp = √3 Vl Il( cos + j sin 라라라라“1” 임)
●
역률 p·f = P / P
a = cos
●
무효율 r·f = P
r / Pa = sin
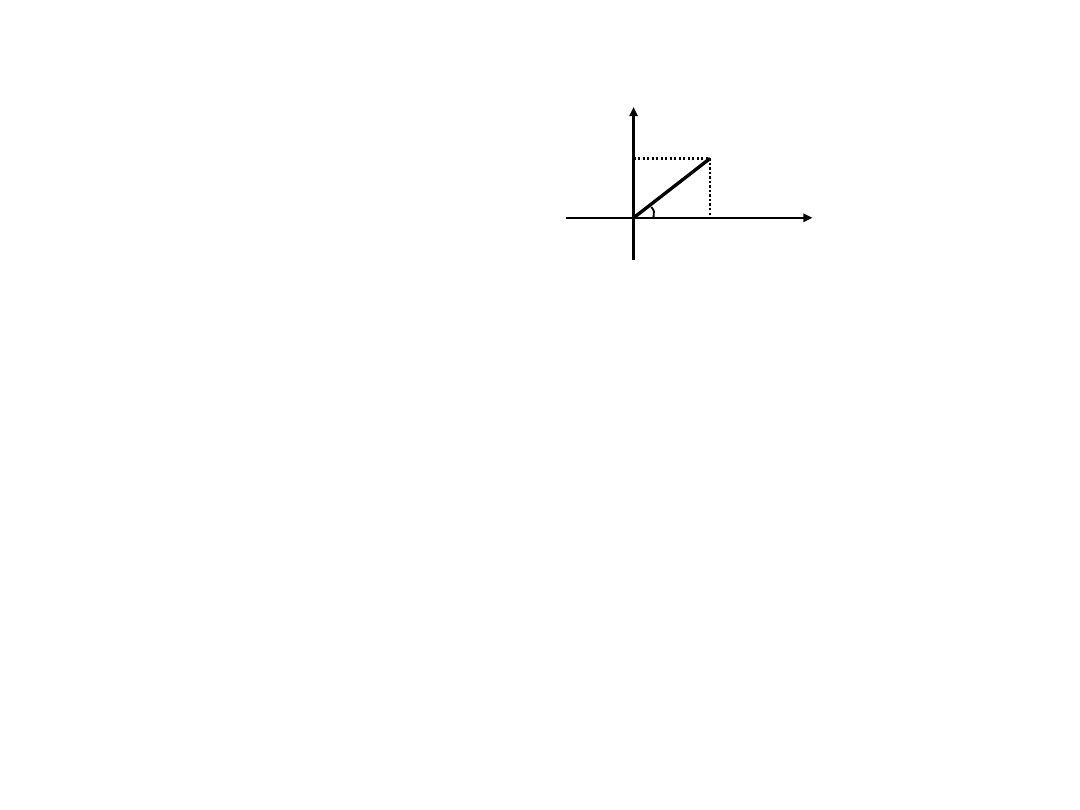
예제12-4) 한 상의 임피던스가 (3+j4) [] 인 평형 3상 Y 부하에 220 [V] 의
선간전압이 인가되어 있을 때, 선전류, 3상전체에 대한 유효전력, 무효전력,
피상전력, 역률 및 무효율을 구하시오.
Y
결선에서,
I = V
p / Z = 220 [V] / 5√3 = 25.4 [A]
=(3+j4) []
이므로, cos = 3/5
Z
·
3
j4
P = 3 V
pIp cos √3 Vl Ilcos
P
r= 3 VpIp sin √3 Vl Ilsin
P
a= √3 Vl Il
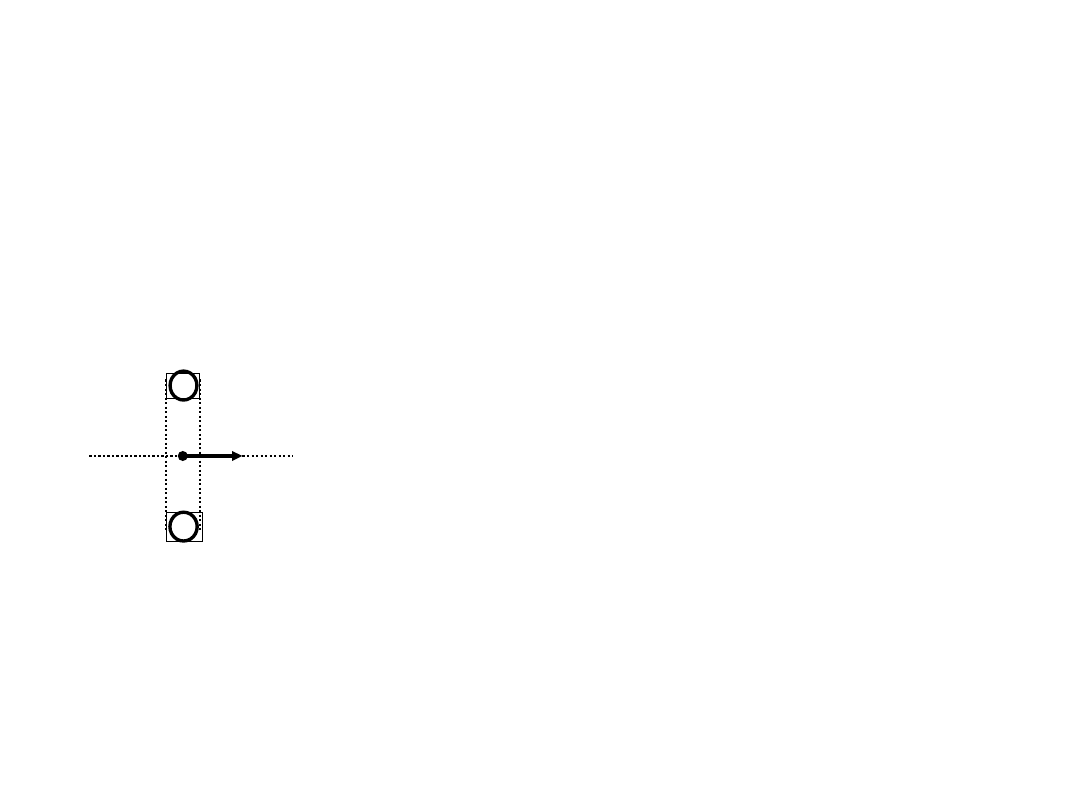
12.8
회전자계
►전류가 흐르면 주변에 자계가 발생하며,
►자계의 세기는 전류세기에 비례 앙페르의 법칙
►교류는 전류의 크기가 시간에 따라 변하므로, 따라서 발생하는
자계도 시간에 따라 변하며, 이를 교번자계(alternating magneticfield) 라 한다.
☞교번자계(alternating magneticfield)
●아래의 단상 교류에서 발생하는 자계를 중심선 OO’ 에서 고려하면,
●
X
O
O’
h
단상 교류의 전류 i =
∴ h =
► n
개의 코일에 n상의 교류를 흘려주면,
각상에서 발생한 자계를 합한 합성자계는
공간을 회전하게 된다.
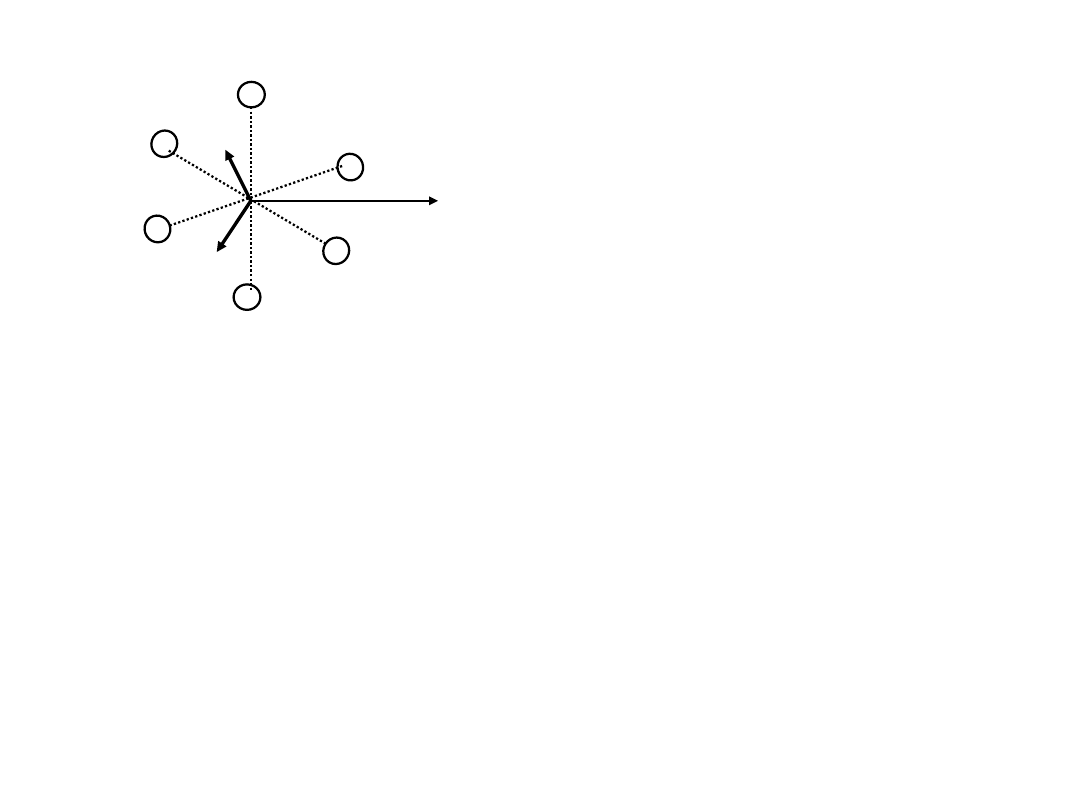
A
●
x
B
●
x
C
●
x
h
a
h
b
h
c
x
► 1200
씩 배치된 3상 코일에 평형전류를 흘렸을 때,
발생하는 자계를 각각 h
a , hb ,hc 라 하면,
h
a =
h
b =
h
c =
► 합성자계를 x 축과 y 축 성분에 대해 각각 합산해서 구하면,
h
x = hax + hbx + hcx
=H
m sin t + Hm sin (t - 120
0
) cos ( - 1200) + H
m sin (t + 120
0
) cos 1200
h
y = hay + hby + hcy
= 0 + H
m sin (t - 120
0
) sin ( - 1200) + H
m sin (t + 120
0
) sin 1200

h
x = Hm sin t
2
3
h
y = Hm cos t
2
3
► 자계의 크기 h는; h = (h
x
2
+ h
y
2
) ½
그리고 tan = h
y / hx = cos t / sin t
=
∴
► 페이저로 표기하면,
☞ 합성자계의 크기는 한 코일에서 생기는 최대자계의 3/2 배,
☞ 교류의 각속도와 같은 회전속도를 가지며
,
☞ 이를 “회전자계”라 한다
.
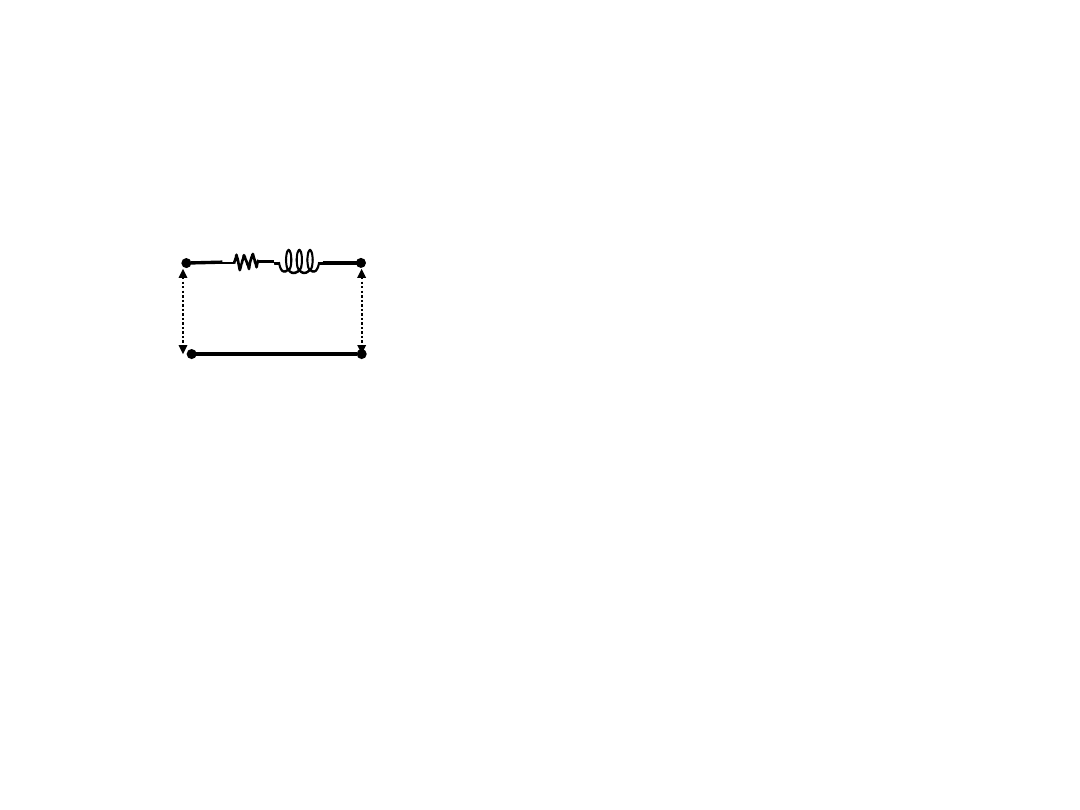
12.9
선로의 전압 강하
► 선로의 임피던스로 인해 전압 강하가 발생한다.
따라서 부하에 적절한 전압을 공급하기 위해서는
전원의 공급전압과 선로의 전압강하를 고려하여야 한다.
R
X
V
s
V
r
<
전선의 임피던스 >
V
s는 송전단 전압 Vr은 수전단 전압
R
과 X는 전선 한가닥의 저항과 리액턴스
I
는 선전류, q는 위상각
► 전압강하 e =
[1]
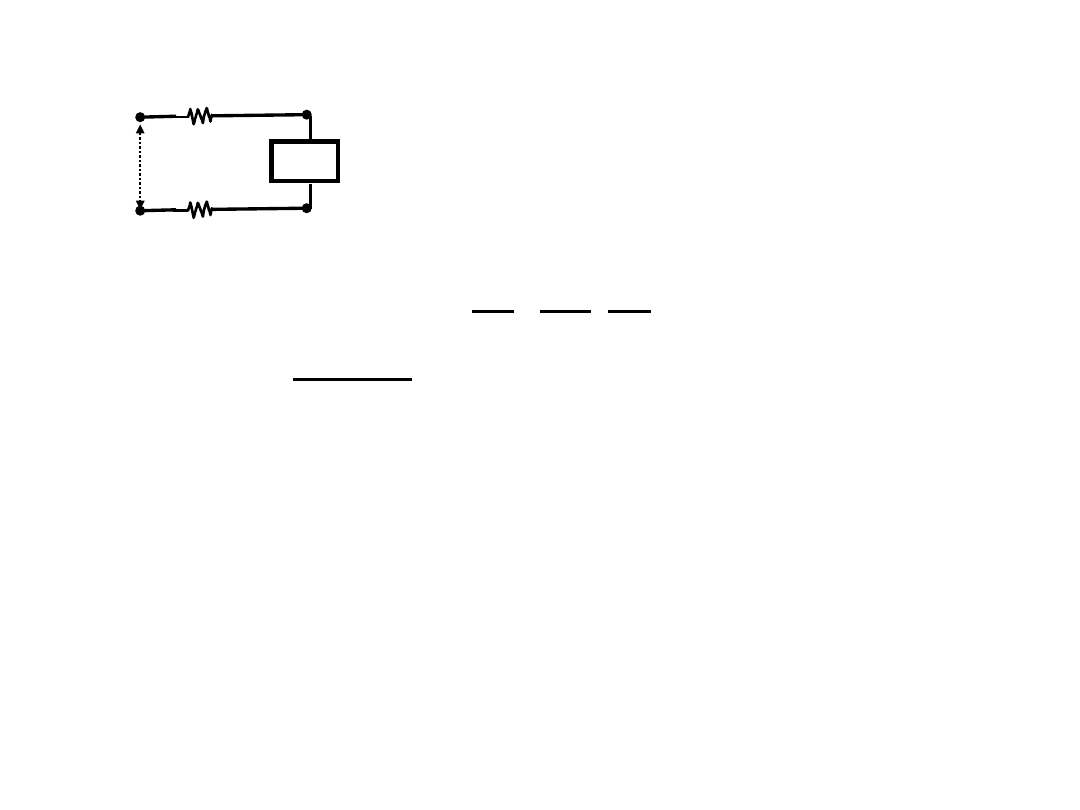
단상 2선식의 전압 강하
R
V
s
부하
R
► 전압강하 e = V
s – Vr = 2RI = · · · 2I
58
1
97
100
A
L
1000A
35.6 LI
= [V]
A[mm2], L[m] :
도체의 단면적과 선로의 길이
표준연동의 고유저항 (1/58) x 10-6 [·m]
전선의 도전율 97 % 로 계산
예제12-5) 단상 2선식 선로에 10[A]가 흐르고 있을 때
도체의 단면적이 10 [mm2], 선로 길이가 100 [m]라면
전압강하는 ?
전압강하 =

[2] 3
상 3선식의 전압 강하
► 전압강하 e = V
s – Vr = · · · I · √3
58
1
97
100
A
L
1000A
30.8 LI
= [V]
예제12-6) 3상 3선식 선로에 10[A]가 흐르고 있을 때
도체의 단면적이 10 [mm2], 선로 길이가 1000 [m]라면
전압강하는 ?

[3] 3
상 4선식의 전압 강하
► 전압강하 e = V
s – Vr = RI = · · · I
58
1
97
100
A
L
1000A
17.8 LI
= [V]
예제12-6) 3상 4선식 선로에 50[A]가 흐르고 있을 때
도체의 단면적이 100 [mm2], 선로 길이가 2000 [m]라면
전압강하는 ?
► 평형 3상4선식으로 중성선에 전류가 흐르지 않는 다는 가정