
수 학 (6면 중
2 면)
2015학년도 중등학교교사 임용후보자 선정경쟁시험
수 학
수험 번호 : (
)
성 명 : (
)
제1차 시험
2 교시 전공A
14문항 40점
시험 시간 90분
◦ 문제지 전체 면수가 맞는지 확인하시오.
◦ 모든 문항에는 배점이 표시되어 있습니다.
기입형 【1 ~ 10】
1. 중학교 기하 수업에서 다음과 같은 자료를 이용하여 정사면체에
대해 학습하였다.
< 빨대로 만든 정사면체 >
< 종이로 만든 정사면체 >
< 자석막대로 만든 정사면체 >
< 정사면체 모양의 지갑 >
위 자료들은 서로 다르게 보이지만, 구조적으로는 같은 구체물이다.
딘즈(Z. Dienes)의 수학 학습 이론에서 볼 때, 이러한 다양한 형태의
구체물을 활용한 수업은 어떤 원리를 적용한 것인지 쓰시오. [2점]
2. 다음 그림과 같이 반시계 방향의 단순닫힌곡선(simple closed curve)
:
가 주어졌을 때,
sin cos 의 값을 구하시오. [2점]
3. 매개변수방정식
, ( ≤ ≤ )로 주어진
곡선 가 있다. 이 곡선 위의 두 점 , 을
연결하는 직선의 기울기와 곡선 위의 점 에서의 접선의
기울기가 같게 되는 값 를 구간 에서 구하시오. [2점]

수 학 (6면 중
3 면)
4. 좌표공간 ℝ
에서 원점과 점 을 지나는 직선을 회전축으로
하여 ° 회전이동하는 변환을 라 하자. 벡터 에 대하여
가 되는 행렬 의 특성다항식(고유다항식,
characteristic polynomial)을 구하시오. [2점]
5. 모집단 는 어떤 지역의 세 남자들로 이루어져 있다. 모집단 에
속하는 남자의 키는 평균 cm, 표준편차 cm인 정규분포를 따른
다고 한다. 모집단 에서 임의로 뽑은 남자의 키cm와 몸무게kg를
각각 확률변수 , 라 할 때,
가 성립한다고 하자.
여기서, 는 평균 , 표준편차
인 정규분포를 따르는 확률변수
이고, 와 는 독립이다. 확률 P P 일 때, 의 값
을 구하시오. (단, 는 표준정규분포를 따르는 확률변수이다.)
[2점]
6. 두 연속확률변수 와 는 독립이고, 와 의 확률밀도함수
(probability density function)를 각각 ,
이라고 하자.
라 할 때, 확률 P
를 구하시오. (단, 는 보다 크지 않은 최대정수이다.) [2점]
7. 좌표공간 ℝ
에서 두 곡선 이
합동이 되도록 하는 두 상수 에 대하여,
의 값을 구하시오.
[2점]

수 학 (6면 중
4 면)
8. 덧셈군
× 에서 ∈ 로 생성된 부분군을 라 하자.
잉여군(quotient group, factor group) 에서 원소 의
위수(order)를 구하시오. [2점]
9. 실수 전체의 집합 ℝ에 다음 조건 ①, ②에 의해 정의되는 부분집합족
(family of subsets) ℬ를 기저로 하는 위상 가 주어졌다고 하자.
① 모든 정수 에 대하여, ∈ℬ이다.
② 모든 정수 과 음이 아닌 모든 정수 에 대하여,
∈ℬ이다.
위상공간 ℝ 에서 집합
의 도집합(derived set) ′을
구하시오. [2점]
10. 자연수 전체의 집합 에 대하여,
집합 ∈× ≥ 또는 ≥ 에 다음과 같이
위상 가 주어졌다고 하자.
⊆ 는 유한집합∪∅
함수 → 을 으로 정의하고, 의 위상을
⊆
∈라 하자. 위상공간
의 연결성분
(connected component)의 개수를 구하시오. [2점]
수 학 (6면 중
5 면)
서술형 【1 ~ 4】
1. 다음은 박 교수가 수학 교육론 강의 시간에 라카토스(I. Lakatos)의
준경험주의를 주제로 진행한 강의의 일부이다.
박 교수 : 하나의 추측을 제기하고, 그 추측을 부분추측으로 분해
하는 1가지 사례를 말해 봅시다.
민
태 : 교수님, 제가 말해 보겠습니다. 방정식
은
두 실근을 가진다는 추측을 제기하고, 다음과 같이
세 단계로 분해하여 보았습니다.
단계 : 함수
의 그래프는 포물선이고,
실근의 개수는 그래프가 축과 만나는 점의
개수와 같습니다.
단계 : 그래프의 꼭짓점 는
인데, 의 부호를 기준으로 생각하면, 일 때
, 이고, 일 때 , 입니다.
단계 : 포물선의 모양을 생각하면, 일 때 꼭짓점이
제사분면, 일 때 꼭짓점이 제사분면에
있으므로 그래프가 축과 만나는 점은 개입니다.
박 교수 : 민태가 제기한 추측을 통해 라카토스의 준경험주의
관점에서 수업을 진행해 봅시다.
혜
수 : 교수님, ㉠ 방정식 은 근이 이고,
하나의 실근만을 가집니다.
학 생 들 : 맞아요. 민태의 처음 추측이 틀렸어요.
현
덕 : 저는 다르게 생각합니다. ㉡ 어떤 추측이 항상 참이
된다고는 생각하지 않습니다. 그러나 지금 이 경우에는
혜수가 말한 것을 예외로 인정하면 민태의 추측을 옹호
할 수 있습니다.
박 교수 : 어디 한번 봅시다. 만약 혜수의 말이 옳다면, 민태의
부분추측은 어디가 잘못되었을까요?
혜
수 : 단계가 잘못된 것 같습니다. 일 때 의 값을
함께 고려해 보겠습니다. 만약 이면 이
아니라
이 됩니다.
박 교수 : 그렇군요. 그러면 부분추측을 수정해야겠군요. 단계와
단계를 합쳐서 수정해 봅시다. 그리고 처음의 추측도
수정해야겠군요.
은
영 : 교수님, 1단계도 이상한데요? 함수
의
그래프는 항상 포물선인가요?
혜
수 : 아닌 것 같습니다.
… (중략) …
민
태 : 교수님, 지금까지의 논의를 통해 볼 때 다음과 같이
정리할 수 있습니다. ≠인 방정식
은
일 때, 두 실근을 갖습니다.
위 상황에서 ㉡의 관점에서 ㉠과 같은 반례가 출현할 때, 이 반례에
대한 라카토스의 대응 방법을 무엇이라고 부르는지 적고, 이러한
대응 방법으로 인해 발생할 수 있는 현상에 대해 쓰시오. 또,
위 강의 내용을 참고하여 라카토스의 준경험주의 관점에서 수학적
지식의 성장 과정을 설명하시오. [5점]
2. 다음은 김 교사가 정 교사의 수업을 참관한 후, 김 교사가 작성한
수업참관일지와 정 교사가 작성한 수업소감문의 일부이다.
(가) 김 교사의
정 교사는 도입 단계에서 다음과 같은 사실을 제시하여
학생의 학습 동기를 유발하고자 하였다.
이로부터, “연속한 홀수의 합은 어떤 수의 제곱이 될까?”라고
발문을 하면서,
⋯
이라는 탐구과제를 학생들에게 제시하였다. 학생들은 이 탐구
과제를 수행하는 과정에서 아래와 같은 특수한 몇몇 사례를
조사하였다.
학생들은 구체적인 사례에 대한 관찰로부터 새로운 추측
⋯
을 발견하였다. 이러한 발견 이후,
㉠ 정 교사는 수학적 귀납법을 이용하여 탐구과제에 대한 수업을
계속 진행
하였다.
… (후략) …
(나) 정 교사의
학생들은 자신들이 관찰한 구체적인 사례로부터 공통점에
주목하여 새로운 추측을 잘 이끌어 내었다. 하지만, 조금 아쉬운
점은 ㉡ ⋯ 이 성립함을 보여 주는
시각적 모형(visual model)
을 학생들에게 제공해 주지 못했다는
것이다.
위의
를 통해 볼 때, 정 교사의 수업에서 학생들이
사용했을 추론 유형을 적고, 이 추론 유형의 특성에 근거하여
㉠의 이유를 설명하시오. 또,
에 제시된 ㉡에 해당하는
구체적인 예를 하나 제시하시오. [5점]
수 학 (6면 중
6 면)
<수고하셨습니다.>
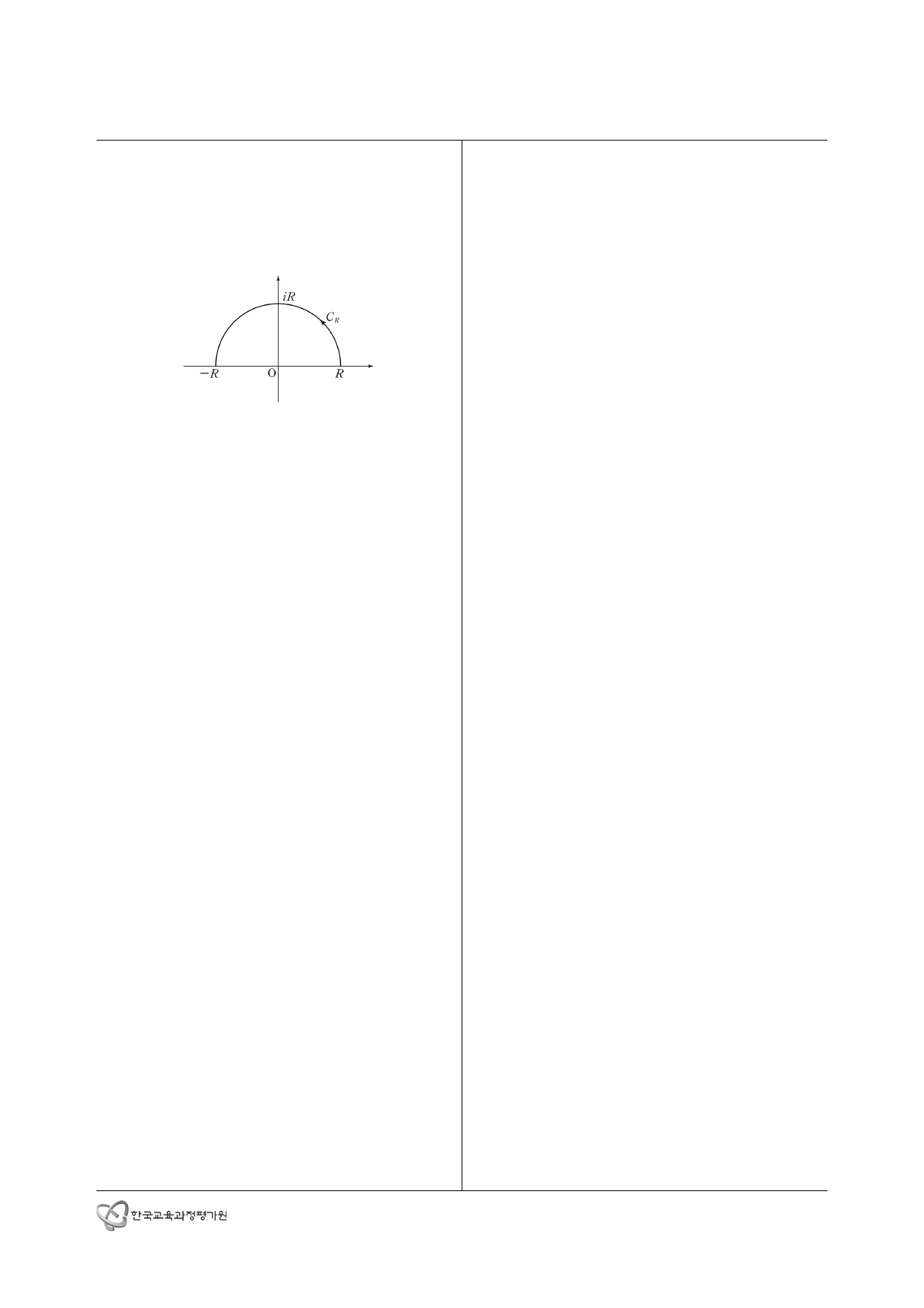
3. 복소평면 에서 다음 그림과 같이 반지름의 길이가 인 반원을
∈ ≤ ≤ 라고 할 때, 과 에 대하여
lim
→ ∞
임을 보이고
∞
∞
의 값을
풀이 과정과 함께 쓰시오. [5점]
4. 다음 삼차 합동방정식에 대하여
에 속하는 해의 개수를
풀이 과정과 함께 쓰시오. [5점]
≡ mod (참고 : × × )